
 的圖象與拋物線y=x2+(9m+4)x+m-
的圖象與拋物線y=x2+(9m+4)x+m- 1交于點A(3,n).
1交于點A(3,n). (x>0)的圖象于點C,且AC=2AB,求B、C兩點的坐標;
(x>0)的圖象于點C,且AC=2AB,求B、C兩點的坐標;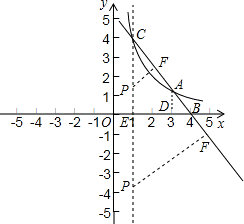 解:(1)∵點A(3,n)在反比例函數(shù)
解:(1)∵點A(3,n)在反比例函數(shù) 的圖象上,
的圖象上, ,
, ).
). )在拋物線y=x2+(9m+4)x+m-1上,
)在拋物線y=x2+(9m+4)x+m-1上, =9+(9m+4)×3+m-1,
=9+(9m+4)×3+m-1, .
. ;
;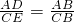 .
.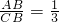 .
. ,
,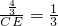 .
.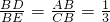 ,DE=2,
,DE=2,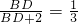 .
.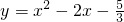 的對稱軸是x=1,
的對稱軸是x=1,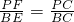 .
.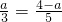 .解得
.解得 .
. ).
).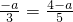 .解得a=-6.
.解得a=-6. )或(1,-6).
)或(1,-6). 的圖象上,即可求得n的值,又由點A在拋物線y=x2+(9m+4)x+m-1上,利用待定系數(shù)法即可求得;
的圖象上,即可求得n的值,又由點A在拋物線y=x2+(9m+4)x+m-1上,利用待定系數(shù)法即可求得;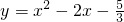 的對稱軸,證得:△PCF∽△BCE,再分別從當點P在第一象限內(nèi)時,設P(1,a)(a>0)與當點P在第四象限內(nèi)時,設P(1,a)(a<0)利用相似三角形的對應邊成比例求解即可.
的對稱軸,證得:△PCF∽△BCE,再分別從當點P在第一象限內(nèi)時,設P(1,a)(a>0)與當點P在第四象限內(nèi)時,設P(1,a)(a<0)利用相似三角形的對應邊成比例求解即可.

 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數(shù)學 來源: 題型:
| 4 |
| 9 |
2
| ||
| 5 |
| HE |
| HF |
| 1 |
| 2 |
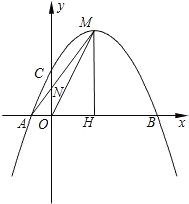 直線QG的解析式;若不存在,請說明理由.
直線QG的解析式;若不存在,請說明理由.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
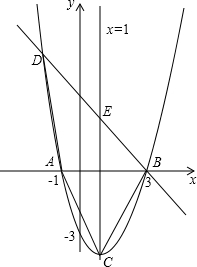 點B在A點的右側;交y軸于(0,-3).
點B在A點的右側;交y軸于(0,-3).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
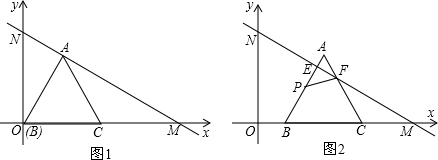
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 ,對稱軸l與x軸相交于點C,頂點為點D,且∠ADC的正切值為
,對稱軸l與x軸相交于點C,頂點為點D,且∠ADC的正切值為| 1 | 2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 如圖①,在等腰直角三角板ABC中,斜邊BC為2個單位長度,現(xiàn)把這塊三角板在平面直角坐標系xOy中滑動,并使B、C兩點始終分別位于y軸、x軸的正半軸上,直角頂點A與原點O位于BC兩側.
如圖①,在等腰直角三角板ABC中,斜邊BC為2個單位長度,現(xiàn)把這塊三角板在平面直角坐標系xOy中滑動,并使B、C兩點始終分別位于y軸、x軸的正半軸上,直角頂點A與原點O位于BC兩側.| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com