
【題目】如圖,AH是⊙O的直徑,矩形ABCD交⊙O于點E,連接AE,將矩形ABCD沿AE折疊,點B落在CD邊上的點F處,畫直線EF. 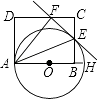
(1)求證:直線EF是⊙O的切線.
(2)若CD=10,EB=5,求⊙O的直徑.
【答案】
(1)證明:
如圖,連接OE,
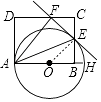
∵OA=OE,
∴∠EAO=∠AEO,
由折疊可得∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
在矩形ABCD中,∠ABC=90°,
由折疊可知∠AFE=∠ABC=90°,
∴∠OEF=90°,
∴OE⊥EF,且點E在圓上,OE為半徑,
∴EF是⊙O的切線
(2)解:∵四邊形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
設OA=OE=x,則OB=10﹣x,
在Rt△OBE中,∠OBE=90°,EB=5,
由勾股定理可得OB2+BE2=OE2,
∴(10﹣x)2+52=x2,解得x= ![]() ,
,
∴AH=2x= ![]() ,
,
∴⊙O的直徑為 ![]()
【解析】(1)連接OE,由折疊的性質結合條件可證得OE∥AF,再由條件可得AF⊥EF,則可證得結論;(2)可設OA=OE=x,則OB=10﹣x,在Rt△OBE中,可求得x的值,進一步可求得⊙O的直徑.
【考點精析】本題主要考查了矩形的性質和翻折變換(折疊問題)的相關知識點,需要掌握矩形的四個角都是直角,矩形的對角線相等;折疊是一種對稱變換,它屬于軸對稱,對稱軸是對應點的連線的垂直平分線,折疊前后圖形的形狀和大小不變,位置變化,對應邊和角相等才能正確解答此題.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
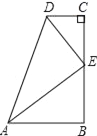
【題目】在數學活動課上,小明提出這樣一個問題:如圖,∠B=∠C=90°,E是BC的中點,DE平分∠ADC,∠CED=35°,則∠EAB的度數是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店分兩次購進![]() 、
、![]() 兩種商品進行銷售,兩次購進同一種商品的進價相同,具體情況如下表所示:
兩種商品進行銷售,兩次購進同一種商品的進價相同,具體情況如下表所示:
購進數量(件) | 購進所需費用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 兩種商品每件的進價分別是多少元?
兩種商品每件的進價分別是多少元?
(2)商場決定![]() 種商品以每件30元出售,
種商品以每件30元出售,![]() 種商品以每件100元出售.為滿足市場需求,需購進
種商品以每件100元出售.為滿足市場需求,需購進![]() 、
、![]() 兩種商品共1000件,且
兩種商品共1000件,且![]() 種商品的數量不少于
種商品的數量不少于![]() 種商品數量的4倍,請你求出獲利最大的進貨方案,并確定最大利潤.
種商品數量的4倍,請你求出獲利最大的進貨方案,并確定最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
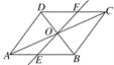
【題目】如圖,在平行四邊形ABCD中,對角線AC,BD交于點O,經過點O的直線交AB于E,交CD于F,AB=4,AD=3,OF=1.3.求四邊形BCFE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,四邊形ABCD的四個頂點分別在格點上.
(1)畫出四邊形ABCD關于x軸對稱的圖形A′B′C′D′.
(2)將四邊形ABCD向右平移得到四邊形A″B″C″D″,使得△BB′B″為等腰直角三角形,畫出四邊形A″B″C″D″,并寫出點C″的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著“互聯網+”時代的到來,一種新型打車方式受到大眾歡迎,該打車方式的總費用由里程費和耗時費組成,其中里程費按![]() 元/公里計算,耗時費按
元/公里計算,耗時費按![]() 元/分鐘計算(總費用不足
元/分鐘計算(總費用不足![]() 元按
元按![]() 元計價).小敏、小剛兩人用該打車方式出行,按上述計價規則,其行駛里程數、耗時以及打車總費用如下表:
元計價).小敏、小剛兩人用該打車方式出行,按上述計價規則,其行駛里程數、耗時以及打車總費用如下表:
里程數 | 耗時 | 車費(元) | |
小敏 |
|
|
|
小剛 |
|
|
|
![]() 求
求![]() 的值;
的值;
![]() 若小華也用該打車方式打車,平均車速為
若小華也用該打車方式打車,平均車速為![]() 公里/時,行駛了
公里/時,行駛了![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
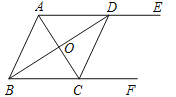
【題目】如圖,AE∥BF,AC平分∠BAE,且交BF于點C,BD平分∠ABF,且交AE于點D,AC與BD相交于點O,連接CD
(1)求∠AOD的度數;
(2)求證:四邊形ABCD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學學生會為了考察該校1800名學生參加課外體育活動的情況,采取抽樣調查的方法從“籃球、排球、乒乓球、足球及其他”等五個方面調查了若干名學生的興趣愛好(每人只能選其中一項),并將調查結果繪制成如下兩幅不完整的統計圖,請根據圖中提供的信息,下列判斷:①本次抽樣調查的樣本容量是60;②在扇形統計圖中,“其他”部分所對應的圓心角是60°;③該校學生中喜歡“乒乓球”的人數約為450人;④若被抽查的男女學生數相同,其中喜歡球類的男生占喜歡球類人數的56.25%,則被抽查的學生中,喜歡“其他”類的女生數為9人.其中正確的判斷是( )

A. 只有①②③B. 只有①②④C. 只有①③④D. 只有③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于二次函數y=x2-3x+2和一次函數y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)稱為這兩個函數的“再生二次函數”,其中t是不為零的實數,其圖象記作拋物線E.
現有點A(2,0)和拋物線E上的點B(-1,n),請完成下列任務: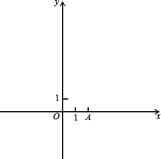
(1)【嘗試】
①當t=2時,拋物線E的頂點坐標是.
②點A拋物線E上;(填“在”或“不在”),
③n=.
(2)【發現】通過②和③的演算可知,對于t取任何不為零的實數,拋物線E總過定點,這個定點的坐標是.
(3)【應用1】二次函數y=-3x2+5x+2是二次函數y=x2-3x+2和一次函數y=-2x+4的一個“再生二次函數”嗎?如果是,求出t的值;如果不是,說明理由.
(4)【應用2】以AB為一邊作矩形ABCD,使得其中一個頂點落在y軸上,若拋物線E經過點A、B、C,求出所有符合條件的t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com