
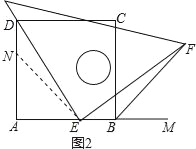
【題目】如圖所示,四邊形ABCD是正方形,M是AB延長線上一點.直角三角尺的一條直角邊經過點D,且直角頂點E在AB邊上滑動(點E不與點A、B重合),另一直角邊與∠CBM的平分線BF相交于點F.

(1)如圖1,當點E在AB邊得中點位置時:
①通過測量DE、EF的長度,猜想DE與EF滿足的數(shù)量關系是 .
②連接點E與AD邊的中點N,猜想NE與BF滿足的數(shù)量關系是 ,請證明你的猜想.
(2)如圖2,當點E在AB邊上的任意位置時,猜想此時DE與EF有怎樣的數(shù)量關系,并證明你的猜想.
【答案】(1)①DE=EF;②NE=BF;理由見解析;(2)DE=EF,理由見解析.
【解析】試題分析:(1)根據(jù)正方形的性質及N,E分別為AD,AB的中點可得DN=EB,再根據(jù)角平分線的性質及AN=AE可得∠DNE=∠EBF=135°,從而可證得△DNE≌△EBF,繼而證得結論;
(2)在DA邊上截取DN=EB,連結NE,點N就使得NE=BF成立,由DN=EB可得AN=AE,根據(jù)角平分線的性質可得∠DNE=∠EBF=90°+45°=135°,通過證△DNE≌△EBF,從而得結論.
(1)①DE=EF;②NE=BF;理由如下:
∵四邊形ABCD為正方形,∴AD=AB,∠DAB=∠ABC=90°,∵N,E分別為AD,AB中點,
∴AN=DN=![]() AD,AE=EB=
AD,AE=EB=![]() AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,
AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,
又∵∠ADE+∠AED=90°,∴∠FEB=∠ADE,又∵AN=AE,∴∠ANE=∠AEN,又∵∠A=90,∴∠ANE=45°,∴∠DNE=180°﹣∠ANE=135°,又∵∠CBM=90°,BF平分∠CBM,
∴∠CBF=45°,∠EBF=135°,在△DNE和△EBF中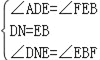 , ∴△DNE≌△EBF(ASA),∴DE=EF,NE=BF.
, ∴△DNE≌△EBF(ASA),∴DE=EF,NE=BF.
(2)DE=EF,理由如下:
在DA邊上截取DN=EB,連接NE,∵四邊形ABCD是正方形,DN=EB,∴AN=AE,∴△AEN為等腰直角三角形,∴∠ANE=45°,∴∠DNE=180°﹣45°=135°,∵BF平分∠CBM,AN=AE,∴∠EBF=90°+45°=135°,∴∠DNE=∠EBF, ∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF,在△DNE和△EBF中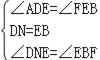 ,∴△DNE≌△EBF(ASA), ∴DE=EF.
,∴△DNE≌△EBF(ASA), ∴DE=EF.


科目:初中數(shù)學 來源: 題型:
【題目】同學們都知道![]() 表示5與(-2)之差的絕對值,也可理解為5與-2兩數(shù)在數(shù)軸上所對的兩點之間的距離,試探索:
表示5與(-2)之差的絕對值,也可理解為5與-2兩數(shù)在數(shù)軸上所對的兩點之間的距離,試探索:
(1) 求![]() = ;
= ;
(2) 使得![]() =3成立的數(shù)是 ;
=3成立的數(shù)是 ;
(3) 由以上探索猜想,對于任何有理數(shù)x,則![]() 最小值是 ;
最小值是 ;
(4)由以上探索猜想,使得![]() 的成立的整數(shù)x是
的成立的整數(shù)x是
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】計算:
(1)![]() ;
;
(2)![]() ;
;
(3)(-36)÷(+12)-(-4)×(-0.5);
(4)(1-![]() +
+![]() )×(-48);
)×(-48);
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)18+42÷(-2)-(-3)2×5;
(9)![]() ×[-32÷(-
×[-32÷(-![]() )2+(-2)3] ;
)2+(-2)3] ;
(10)![]() ;
;
(11)![]()
(12)![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖①,直線y=-![]() x+3與x軸相交于點A,與y軸相交于點B,點C(m,n)是第二象限內一點,以點C為圓心的圓與x軸相切于點E,與直線AB相切于點F.
x+3與x軸相交于點A,與y軸相交于點B,點C(m,n)是第二象限內一點,以點C為圓心的圓與x軸相切于點E,與直線AB相切于點F.
(1)當四邊形OBCE是矩形時,求點C的坐標;
(2)如圖②,若⊙C與y軸相切于點D,求⊙C的半徑.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上運動(
上運動(![]() 不與
不與![]() 、
、![]() 重合),連接
重合),連接![]() ,作
,作![]() ,
,![]() 交線段
交線段![]() 于
于![]() .
.


(1)當![]() 時,
時,![]() = ,
= ,![]() = ;點
= ;點![]() 從
從![]() 向
向![]() 運動時,
運動時,![]() 逐漸 (填“增大”或“減小”);
逐漸 (填“增大”或“減小”);
(2)當![]() 等于多少時,
等于多少時,![]() ,請說明理由;
,請說明理由;
(3)在點![]() 的運動過程中,
的運動過程中,![]() 的形狀可以是等腰三角形嗎?若可以,請直接寫出
的形狀可以是等腰三角形嗎?若可以,請直接寫出![]() 的度數(shù).若不可以,請說明理由.
的度數(shù).若不可以,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在![]() 中,
中, ![]() ,
, ![]() ,將
,將![]() 繞點
繞點![]() 沿逆時針方向旋轉
沿逆時針方向旋轉![]() 得到
得到![]() .
.

(1)線段![]() 的長是 ,
的長是 , ![]() 的度數(shù)是 ;
的度數(shù)是 ;
(2)連結![]() ,求證:四邊形
,求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(3)求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)y=a![]() -4x+c的圖像經過點A和點B.
-4x+c的圖像經過點A和點B.

(1)求該二次函數(shù)的表達式;
(2)寫出該拋物線的對稱軸及頂點坐標;
(3)點P(m,m)與點Q均在該函數(shù)圖像上(其中m>0),且這兩點關于拋物線的對稱軸對稱,求m的值及點Q到x軸的距離
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
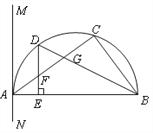
【題目】如圖,△ABC內接于半圓,AB是直徑,過A作直線MN,若∠MAC=∠ABC.
(1)求證:MN是半圓的切線;
(2)設D是弧AC的中點,連結BD交AC 于G,過D作DE⊥AB于E,交AC于F.求證:FD=FG.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,∠A=90°,AB=AC,∠ABC的角平分線交AC于D,BD=4![]() ,過點C作CE⊥BD交BD的延長線于E,則CE的長為( )
,過點C作CE⊥BD交BD的延長線于E,則CE的長為( )

A.![]() B.2
B.2![]() C.3
C.3![]() D.2
D.2![]()
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com