
【題目】如圖,四邊形ABCD、BEFG均為正方形,
(1)如圖1,連接AG、CE,試判斷AG和CE的數(shù)量和位置關系并證明.
(2)將正方形BEFG繞點B順時針旋轉β角(0°<β<180°),如圖2,連接AG、CE相交于點M,連接MB,當角β發(fā)生變化時,∠EMB的度數(shù)是否發(fā)生變化?若不變化,求出∠EMB的度數(shù);若發(fā)生變化,請說明理由.
(3)在(2)的條件下,過點A作AN⊥MB交MB的延長線于點N,請直接寫出線段CM與BN的數(shù)量關系.

【答案】詳見解析.
【解析】試題分析:
(1)判斷![]() 和
和![]() 的數(shù)量關系,可通過
的數(shù)量關系,可通過![]() 證
證![]() 求解.判斷
求解.判斷![]() 和
和![]() 的位置關系,可延長
的位置關系,可延長![]() 交
交![]() 于點
于點![]() ,求
,求![]() 即可。
即可。
(2)![]() ,理由是:過點
,理由是:過點![]() 作
作![]() ,
,![]() ,利用
,利用![]() 得出
得出![]() ,由全等三角形得到面積相等,而
,由全等三角形得到面積相等,而![]() ,可得出
,可得出![]() ,由到角兩邊距離相等的點在角的平分線上得
,由到角兩邊距離相等的點在角的平分線上得![]() 為
為![]() 的角平分線,再由
的角平分線,再由![]() ,及一對對頂角相等,可得
,及一對對頂角相等,可得![]() ,利用角平分線的定義即可求解.
,利用角平分線的定義即可求解.
(3)![]() .如備用圖,在
.如備用圖,在![]() 上截取
上截取![]() ,由
,由![]() 可得
可得![]() 為等腰直角三角形,由勾股定理得
為等腰直角三角形,由勾股定理得![]() ,然后證
,然后證![]() ,因為
,因為![]() (理由:
(理由:![]() ;由問題2中
;由問題2中![]() 得
得![]() ;以及正方形的邊
;以及正方形的邊![]() .由
.由![]() 可得全等).根據(jù)全等三角形的對應邊相等即可求證.
可得全等).根據(jù)全等三角形的對應邊相等即可求證.
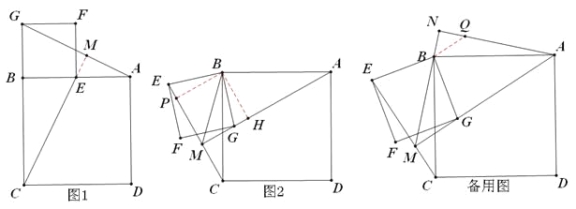
試題解析:
解:(1)![]() ,
,![]() 理由如下:如上圖1,
理由如下:如上圖1,
∵四邊形BEFG和ABCD為正方形
∴![]()
![]()
![]()
![]()
∵在![]() 和
和![]() 中
中
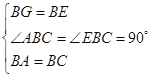
∴![]()
∴![]() ,
,![]()
延長![]() 交
交![]() 于點
于點![]() ,
,
∴![]()
∴![]()
∴![]()
(2)![]() ,理由如下:如上圖2
,理由如下:如上圖2
過點![]() 作
作![]() ,
,![]()
在![]() 和
和![]() 中
中
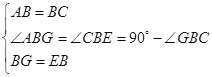
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 平分
平分![]()
∵![]()
∴![]()
(3)![]()


科目:初中數(shù)學 來源: 題型:
【題目】平面內(nèi)有三點A(2,2 ![]() ),B(5,2
),B(5,2 ![]() ),C(5,
),C(5, ![]() ).
).
(1)請確定一個點D,使四邊形ABCD為長方形,寫出點D的坐標.
(2)求這個四邊形的面積(精確到0.01).
(3)將這個四邊形向右平移2個單位,再向下平移3 ![]() 個單位,求平移后四個頂點的坐標.
個單位,求平移后四個頂點的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】要了解全市中考生的數(shù)學成績在某一范圍內(nèi)的學生所占比例的大小,需知道相應樣本的______(填“平均數(shù)”或“頻數(shù)分布”)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示是重疊的兩個直角三角形.將其中一個直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,則圖中陰影部分面積為cm2 . 
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,A(a,0),C(b,2),且滿足(a+b)2+|a﹣b+4|=0,過C作CB⊥x軸于B. 
(1)求三角形ABC的面積.
(2)若過B作BD∥AC交y軸于D,且AE,DE分別平分∠CAB,∠ODB,如圖2,求∠AED的度數(shù). 
(3)在y軸上是否存在點P,使得三角形ABC和三角形ACP的面積相等?若存在,求出P點坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com