
如圖,直線y=![]() 和x軸、y軸的交點分別為B,C.點A的坐標是(-2,0)
和x軸、y軸的交點分別為B,C.點A的坐標是(-2,0)

(1)試說明△ABC是等腰三角形;
(2)動點M從點A出發沿x軸向點B運動,同時動點N從點B出發沿線段BC向點C運動,運動的速度均為每秒1個單位長度,當其中一個動點到達終點時,它們都停止運動,設點運動t秒時,△MON的面積為s.
①求s與t的函數關系式;
②當點M在線段OB上運動時,是否存在s=4的情形?若存在,求出對應的t值;若不存在,說明理由;
③在運動過程中,當△MON為直角三角形時,求t的值.
|
解:(1)將y=0代入y= 將x=0,代入y= 在Rt△OBC中,∵OC=4,OB=3,∴BC=5. 又A(-2,0),∴AB=5,∴AB=BC,∴△ABC是等腰三角形. 4分 (2)∵AB=BC=5,故點M、N同時開始運動,同時停止運動. 過點N作ND⊥x軸于D,則ND=NB·sin∠OBC= 當0<t<2時(如圖甲) OM=2-t, ∴s= =
當2<t≤5時(如圖乙),OM=t-2, ∴s= =
(注:若將t的取值范圍分別寫為0≤t≤2和2≤t≤5,不扣分) ①存在s=4的情形. 當s=4時, 解得t1=1+ ②當MN⊥x軸時,△MON為直角三角形, MB=NB·COS∠MBN= ∴ 當點M,N分別運動到點B,C時,△MON為直角三角形,t=5. 故△MON為直角三角形時,t= |


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
如圖,直線y=kx+k(k≠0)與雙曲線y=![]() 在第一象限內相交于點M,與x軸交于點A.
在第一象限內相交于點M,與x軸交于點A.

(1)求m的取值范圍和點A的坐標;
(2)若點B的坐標為(3,0),AM=5,S△ABM=8,求雙曲線的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
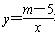 在第一象限內相交于點M,與x軸交于點A.
在第一象限內相交于點M,與x軸交于點A.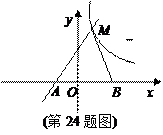
查看答案和解析>>
科目:初中數學 來源:2012屆江蘇省鹽城市解放路學校中考仿真數學卷(帶解析) 題型:解答題
如圖,直線y=kx+k(k≠0)與雙曲線y= 在第一象限內相交于點M,與x軸交于點A.
在第一象限內相交于點M,與x軸交于點A.
(1)求m的取值范圍和點A的坐標;
(2)若點B的坐標為(3,0),AM=5,S△ABM=8,求雙曲線的函數表達式.
查看答案和解析>>
科目:初中數學 來源:2015屆江蘇昆山兵希中學初二上第二次階段測試數學卷(解析版) 題型:解答題
如圖,直線y=kx-2與x軸、y軸分別交于B、C兩點,OB:OC=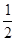 .
.
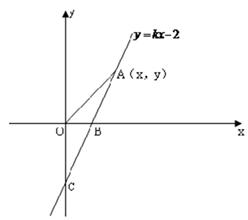
(1)求B點的坐標和k的值.
(2)若點A(x,y)是第一象限內的直線y=kx-2上的一個動點,當點A運動過程中,①試寫出△AOB的面積S與x的函數關系式;②探索:當點A運動到什么位置時,△AOB的面積是1.③在②成立的情況下,x軸上是否存在一點P,使△POA是等腰三角形.若存在,請寫出滿足條件的所有P點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com