
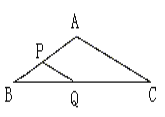
【題目】如圖,在△ABC中(∠B≠∠C),AB=8 cm,BC=16 cm,點P從點A開始沿邊AB向點B以2 cm/s的速度移動,點Q從點B開始沿邊BC向點C以4 cm/s的速度移動,如果點P、Q分別從點A、B同時出發,經幾秒鐘△PBQ與△ABC相似?試說明理由.
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() 、
、![]() ,且與直線
,且與直線![]() 交于點
交于點![]() .
.

(1)若![]() 是線段
是線段![]() 上的點,且
上的點,且![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的函數表達式.
的函數表達式.
(![]() )在(
)在(![]() )的條件下,設
)的條件下,設![]() 是射線
是射線![]() 上的點,在平面內是否存在點
上的點,在平面內是否存在點![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形?若存在,直接寫出點
為頂點的四邊形是菱形?若存在,直接寫出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數y1=-![]() x與反比例函數y2=
x與反比例函數y2=![]() 的圖象經過A(-2,1)點,求:
的圖象經過A(-2,1)點,求:
(1)反比例函數的解析式.
(2)正比例與反比例函數另一個交點B的坐標.
(3)當x在什么范圍,y1=y2,當x在什么范圍,y1<y2,當x在什么范圍,y1>y2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗與探究:
(![]() )由圖觀察易知
)由圖觀察易知![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 的坐標為
的坐標為![]() ,請在圖中分別標明
,請在圖中分別標明![]() 、
、![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 、
、![]() 的位置,并寫出他們的坐標:
的位置,并寫出他們的坐標:![]() __________、
__________、![]() __________.
__________.
歸納與發現:
(![]() )結合圖形觀察以上三組點的坐標,你會發現:坐標平面內任一點
)結合圖形觀察以上三組點的坐標,你會發現:坐標平面內任一點![]() 關于第一、三象限的角平分線
關于第一、三象限的角平分線![]() 的對稱點
的對稱點![]() 的坐標為__________(不必證明).
的坐標為__________(不必證明).
運用與拓廣:
(![]() )已知兩點
)已知兩點![]() 、
、![]() ,試在直線
,試在直線![]() 上確定一點
上確定一點![]() ,使點
,使點![]() 到
到![]() 、
、![]() 兩點的距離之和最小,并求出
兩點的距離之和最小,并求出![]() 點坐標.
點坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個半徑為18 cm的圓,從中心挖去一個正方形,當挖去的正方形的邊長由小變大時,剩下部分的面積也隨之發生變化.
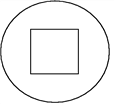
(1)若挖去的正方形邊長為x(cm),剩下部分的面積為y(cm2),則y與x之間的關系式是什么?
(2)當挖去的正方形的邊長由1 cm變化到9 cm時,剩下部分的面積由____變化到____.
查看答案和解析>>
科目:初中數學 來源: 題型:
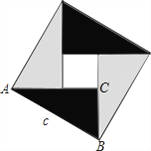
【題目】中國古代數學家們對于勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位,體現了數學研究中的繼承和發展.現用4個全等的直角三角形拼成如圖所示“弦圖”.Rt△ABC中,∠ACB=90°,若![]() ,請你利用這個圖形解決下列問題:
,請你利用這個圖形解決下列問題:
(1)試說明![]() ;
;
(2)如果大正方形的面積是10,小正方形的面積是2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
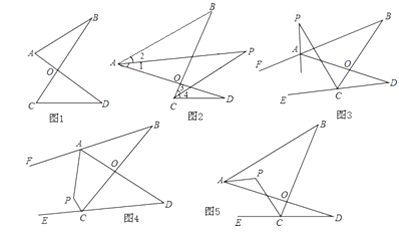
【題目】根據題意解答:(1)如圖1的圖形我們把它稱為“8字形”,請說明∠A+∠B=∠C+∠D.
(2)閱讀下面的內容,并解決后面的問題: 如圖2,AP、CP分別平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度數.
解:∵AP、CP分別平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4
由(1)的結論得:∠P+∠3=∠1+∠B①,∠P+∠2=∠4+∠D②,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P= ![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
①如圖3,直線AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,請猜想∠P的度數,并說明理由.
②在圖4中,直線AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P與∠B、∠D的關系,直接寫出結論,無需說明理由.
③在圖5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P與∠B、∠D的關系,直接寫出結論,無需說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把△ABC紙片沿DE折疊,當點A在四邊形BCDE的外部時,記∠AEB為∠1,∠ADC為∠2,則∠A、∠1與∠2的數量關系,結論正確的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某教研部門為了了解在校初中生閱讀教科書的現狀,隨機抽取某校部分初中學生進行了調查,依據相關數據繪制成以下不完整的統計表,請根據圖表中的信息解答下列問題:
某校初中生閱讀教科書情況統計圖表
類別 | 人數 | 占總人數比例 |
重視 | a | b |
一般 | 57 | 0.285 |
不重視 | c | 0.36 |
說不清楚 | 9 | 0.045 |
(1)求樣本容量及表格中a,b,c的值,并補全統計圖;
(2)若該校共有初中生2500名,請估計該校“重視閱讀教科書”的初中人數;
(3)①根據上面的統計結果,談談你對該校初中生閱讀教科書的現狀的看法及建議;
②如果要了解全省初中生閱讀教科書的情況,你認為應該如何進行抽樣?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com