
 取得最小值-1,并且與y軸交于點C(0,3),與x軸交于點A、B(A在B的右邊)。
取得最小值-1,并且與y軸交于點C(0,3),與x軸交于點A、B(A在B的右邊)。
 ;(2)
;(2) 或
或 ;(3)
;(3)
 ;
;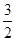 ,
,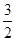 )
)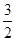
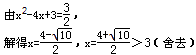


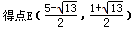
 ,當∠EDF=90°時,E2
,當∠EDF=90°時,E2 ;
;


科目:初中數學 來源:不詳 題型:解答題
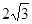 ),∠BCO=60°,OH⊥BC于點H.動點P從點H出發,沿線段HO向點O運動,動點Q從點O出發,沿線段OA向點A運動,兩點同時出發,速度都為每秒1個單位長度.設點P運動的時間為t秒.
),∠BCO=60°,OH⊥BC于點H.動點P從點H出發,沿線段HO向點O運動,動點Q從點O出發,沿線段OA向點A運動,兩點同時出發,速度都為每秒1個單位長度.設點P運動的時間為t秒.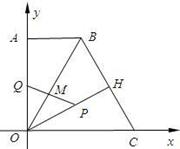
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
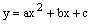 與x軸的另一交點為A,頂點為P,且對稱軸為直線x=2.
與x軸的另一交點為A,頂點為P,且對稱軸為直線x=2.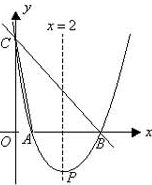
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
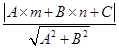 .
.
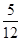 x-
x- 的距離d時,先將y=
的距離d時,先將y=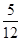 x-
x- 化為5x-12y-2=0,再由上述距離公式求得d=
化為5x-12y-2=0,再由上述距離公式求得d= =
= .
.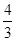 x-4與x軸交于點A,與y軸交于點B,拋物線y=x2-4x+5上的一點M(3,2).
x-4與x軸交于點A,與y軸交于點B,拋物線y=x2-4x+5上的一點M(3,2).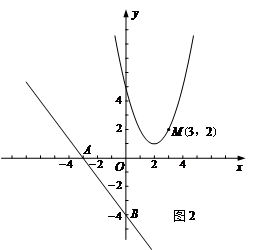
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
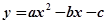 經過梯形的頂點A、B、C、D,已知梯形的兩條底邊長分別為4,6,該拋物線解析式為________________
經過梯形的頂點A、B、C、D,已知梯形的兩條底邊長分別為4,6,該拋物線解析式為________________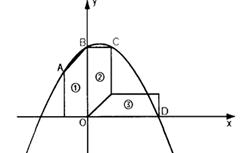
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com