
 如圖所示,直線l:y=3x+3與x軸交于點A,與y軸交于點B.把△AOB沿y軸翻折,點A落到點C,拋物線過點B、C和D(3,0).
如圖所示,直線l:y=3x+3與x軸交于點A,與y軸交于點B.把△AOB沿y軸翻折,點A落到點C,拋物線過點B、C和D(3,0). 解:(1)∵直線l:y=3x+3與x軸交于點A,與y軸交于點B,
解:(1)∵直線l:y=3x+3與x軸交于點A,與y軸交于點B,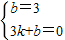 ,
,
 (3+n)•m-
(3+n)•m- ×3×3-
×3×3- (m-3)•n=6,
(m-3)•n=6, ∴P1(4,3),P2(-1,8);
∴P1(4,3),P2(-1,8); (3+m)•(-n)+
(3+m)•(-n)+ ×3×3-
×3×3- (3-n)•m=6,
(3-n)•m=6,

 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:

| 4 |
| n |
| 4 |
| n |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,直線a、b被直線c所截,現給出下列四種條件:①∠2=∠6;②∠2=∠8;③∠1+∠4=180°;④∠3=∠8,其中能判斷是a∥b的條件的序號是( )
如圖所示,直線a、b被直線c所截,現給出下列四種條件:①∠2=∠6;②∠2=∠8;③∠1+∠4=180°;④∠3=∠8,其中能判斷是a∥b的條件的序號是( )查看答案和解析>>
科目:初中數學 來源: 題型:
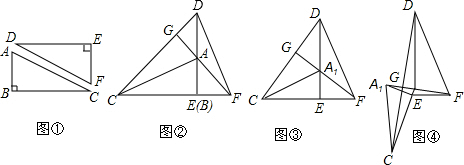
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com