【題目】若一個正整數
能表示成
(
是正整數，且
)的形式，則稱這個數為“明禮崇德數”，
與
是的一個平方差分解. 例如：因為
，所以5是“明禮崇德數”，3與2是5的平方差分解；再如：
(
是正整數)，所以
也是“明禮崇德數”，
與
是的一個平方差分解.
(1)判斷：9_______“明禮崇德數”(填“是”或“不是”)；
(2)已知
(是正整數，
是常數，且
)，要使
是“明禮崇德數”，試求出符合條件的一個值，并說明理由；
(3)對于一個三位數，如果滿足十位數字是7，且個位數字比百位數字大7，稱這個三位數為“七喜數”.若
既是“七喜數”，又是“明禮崇德數”，請求出的所有平方差分解.
【答案】（1）是；（2）k=-5；（3）m=279，
，
.
【解析】
(1)根據9=52-42，確定9是“明禮崇德數”；
(2)根據題意分析N應是兩個完全平方式的差，得到k=-5，將k=-5代入計算即可將N平方差分解，得到答案；
(3)確定“七喜數”m的值，分別將其平方差分解即可.
(1)∵9=52-42，
∴9是“明禮崇德數”，
故答案為：是；
(2)當k=-5時，
是“明禮崇德數”，
∵當k=-5時，
，
=
，
=
，
=
，
=
=
.
∵
是正整數，且
，
∴N是正整數，符合題意，
∴當k=-5時，是“明禮崇德數”；
(3)由題意得：“七喜數”m=178或279，
設m=
=（a+b）（a-b），
當m=178時，
∵178=2
89，
∴
，得
（不合題意，舍去）；
當m=279時，
∵279=393=931，
∴①
，得
，∴，
②
，得
，∴，
∴既是“七喜數”又是“明禮崇德數”的m是279，，.
小學教材全測系列答案
小學數學口算題卡脫口而出系列答案
優秀生應用題卡口算天天練系列答案科目：初中數學 來源： 題型：
【題目】中國派遣三艘海監船在南海保護中國漁民不受菲律賓的侵犯．在雷達顯示圖上，標明了三艘海監船的坐標為
、
、
，（單位：海里）三艘海監船安裝有相同的探測雷達，雷達的有效探測范圍是半徑為
的圓形區域（只考慮在海平面上的探測）．
若在三艘海監船組成的
區域內沒有探測盲點，則雷達的有效探測半徑至少為________海里；
某時刻海面上出現一艘菲律賓海警船
，在海監船
測得點位于南偏東
方向上，同時在海監船
測得位于北偏東
方向上，海警船正以每小時
海里的速度向正西方向移動，我海監船立刻向北偏東
方向運動進行攔截，問我海監船至少以多少速度才能在此方向上攔截到菲律賓海警船？
查看答案和解析>>
科目：初中數學 來源： 題型：
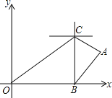
【題目】等腰Rt△ABC中，∠BAC＝90°，AB＝AC,點A、點B分別是y軸、x軸上兩個動點，直角邊AC交x軸于點D，斜邊BC交y軸于點E；
（1）如圖（1），已知C點的橫坐標為-1，直接寫出點A的坐標；
（2）如圖（2）， 當等腰Rt△ABC運動到使點D恰為AC中點時，連接DE，求證：∠ADB＝∠CDE；
（3）如圖（3）， 若點A在x軸上，且A（-4，0），點B在y軸的正半軸上運動時，分別以OB、AB為直角邊在第一、二象限作等腰直角△BOD和等腰直角△ABC，連結CD交y軸于點P,問當點B在y軸的正半軸上運動時，BP的長度是否變化？若變化請說明理由，若不變化，請求出BP的長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學校決定在學生中開設：A、實心球；B、立定跳遠；C、跳繩；D、跑步四種活動項目．為了了解學生對四種項目的喜歡情況，隨機抽取了部分學生進行調查，并將調查結果繪制成如圖①②的統計圖，請結合圖中的信息解答下列問題：
（1）在這項調查中，共調查了多少名學生？
（2）請計算本項調查中喜歡“立定跳遠”的學生人數和所占百分比，并將兩個統計圖補充完整．
（3）若調查到喜歡“跳繩”的5名學生中有2名男生，3名女生，現從這5名學生中任意抽取2名學生，請用畫樹狀圖或列表法求出剛好抽到不同性別學生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在初中階段的函數學習中，我們經歷了“確定函數的表達式——利用函數圖象研究其性質——運用函數解決問題”的學習過程. 在畫函數圖象時，我們通過描點、平移、對稱的方法畫出了所學的函數圖象. 同時，我們也學習了絕對值的意義
，結合上面經歷的學習過程，現在來解決下面的問題
在函數
中，自變量
的取值范圍是全體實數，下表是
與的幾組對應值：
|
| 0 | 1 | 2 | 3 | ||
y | … | 0 | 1 | 2 | 3 | 2 | … |
(1)根據表格填寫：
_______.
(2)化簡函數解析式：
當
時，
_______；
當
時，______.
(3)在給出的平面直角坐標系中，請用你喜歡的方法畫出這個函數的圖象并解決以下問題；
①該函數的最大值為_______.
②若
為該函數圖象上不同的兩點，則
________.
③根據圖象可得關于的方程
的解為_______.
查看答案和解析>>
科目：初中數學 來源： 題型：
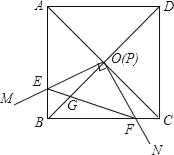
【題目】如圖，邊長為1的正方形ABCD的對角線AC、BD相交于點O．有直角∠MPN，使直角頂點P與點O重合，直角邊PM、PN分別與OA、OB重合，然后逆時針旋轉∠MPN，旋轉角為θ（0°＜θ＜90°），PM、PN分別交AB、BC于E、F兩點，連接EF交OB于點G．
（1）求四邊形OEBF的面積；
（2）求證：OGBD=EF2；
（3）在旋轉過程中，當△BEF與△COF的面積之和最大時，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，AC是弦，點D是弧BC的中點，PD切⊙O于點D．
（1）求證：DP⊥AP；
（2）若PD=
，PC=1，求圖中陰影部分的面積．（結果保留π）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
