
如圖,拋物線 =-
=-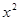 +5
+5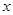 +
+ 經過點C(4,0),與
經過點C(4,0),與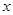 軸交于另一點A,與
軸交于另一點A,與 軸交于點B.
軸交于點B.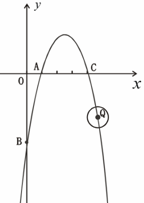
(1)求點A、B的坐標;
(2)P是 軸上一點,△PAB是等腰三角形,試求P點坐標;
軸上一點,△PAB是等腰三角形,試求P點坐標;
(3)若·Q的半徑為1,圓心Q在拋物線上運動,當·Q與 軸相切時,求·Q上的點到點B的最短距離.
軸相切時,求·Q上的點到點B的最短距離.
(1)A(1,0),B(0,-4);(2)P1(0,4),P2(0,-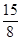 ),P3(0,-4-
),P3(0,-4-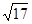 );
);
(3)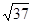 -1
-1
解析試題分析:(1)將C代入 =-
=-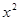 +5
+5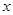 +
+ 即可求得拋物線的解折式,再把
即可求得拋物線的解折式,再把 =0與
=0與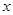 =0代入求得的拋物線的解折式即可求得結果;
=0代入求得的拋物線的解折式即可求得結果;
(2)先根據題意作出圖形,再根據等腰三角形的性質結合勾股定理求解即可;
(3)由題意當Q的橫坐標為1或-1時成立,再代入拋物線解析式即可求得點Q的坐標,連Q1B(即AB),交⊙Q1于M. 連Q2B,交⊙Q2于N,MB和NB即為所求.
(1)將C代入拋物線的解折式得:0=-42+5×4+ ,
, =-4,所以
=-4,所以 =-
=-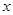 2+5
2+5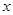 -4
-4
令 =0,則-
=0,則-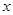 2+5
2+5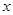 -4=0,解得
-4=0,解得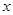 1=4,
1=4, 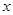 2=1,所以A(1,0)
2=1,所以A(1,0)
令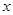 =0,則
=0,則 =-02+5×0-4=-4,所以B(0,-4);
=-02+5×0-4=-4,所以B(0,-4);
(2)如圖,P點有三個.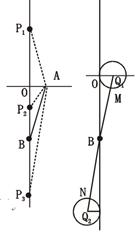
P1(0,4)
令∣P2B∣=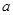 . 則∣0P2∣=4-
. 則∣0P2∣=4-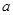
∣P2A∣2=∣0P2∣2+∣0A∣2=(4-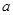 )2+12=
)2+12=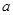 2,解得
2,解得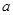 =
=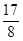
P2(0,-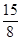 )
)
∣BP3∣=AB=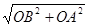 +
+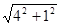 =
=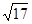
P3(0,-4-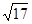 );
);
(3)當Q的橫坐標為1或-1時成立 =-12+5×1-4=0. Q1(1,0)
=-12+5×1-4=0. Q1(1,0) =-(-1)2+5×(-1)-4=-10,Q2(-1,-10)
=-(-1)2+5×(-1)-4=-10,Q2(-1,-10)
連Q1B(即AB),交⊙Q1于M. 連Q2B,交⊙Q2于N,MB和NB即為所求
MB=Q1B-Q1M=AB-QM=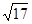 -1
-1
NB=Q2B-Q2N=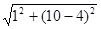 -1=
-1=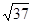 -1.
-1.
考點:二次函數的綜合題
點評:此類問題綜合性強,難度較大,在中考中比較常見,一般作為壓軸題,題目比較典型.


科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2012-2013學年四川省校九年級診斷性檢測數學試卷(解析版) 題型:解答題
如圖,拋物線 =-
=-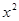 +5
+5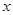 +
+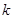 經過點C(4,0),與
經過點C(4,0),與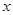 軸交于另一點A,與
軸交于另一點A,與 軸交于點B.
軸交于點B.

(1)求點A、B的坐標;
(2)P是 軸上一點,△PAB是等腰三角形,試求P點坐標;
軸上一點,△PAB是等腰三角形,試求P點坐標;
(3)若·Q的半徑為1,圓心Q在拋物線上運動,當·Q與 軸相切時,求·Q上的點到點B的最短距離.
軸相切時,求·Q上的點到點B的最短距離.
查看答案和解析>>
科目:初中數學 來源:2013年浙江省金華市六校聯誼中考模擬數學試卷(解析版) 題型:填空題
如圖,拋物線y= x2-
x2- x與x軸交于O,A兩點. 半徑為1的動圓(⊙P),圓心從O點出發沿拋物線向靠近點A的方向移動;半徑為2的動圓(⊙Q),圓心從A點出發沿拋物線向靠近點O的方向移動. 兩圓同時出發,且移動速度相等,當運動到P,Q兩點重合時同時停止運動. 設點P的橫坐標為t .
x與x軸交于O,A兩點. 半徑為1的動圓(⊙P),圓心從O點出發沿拋物線向靠近點A的方向移動;半徑為2的動圓(⊙Q),圓心從A點出發沿拋物線向靠近點O的方向移動. 兩圓同時出發,且移動速度相等,當運動到P,Q兩點重合時同時停止運動. 設點P的橫坐標為t .

(1)點Q的橫坐標是 (用含t的代數式表示);
(2)若⊙P與⊙Q 相離,則t的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇省無錫市九年級上學期期末考試數學試卷(解析版) 題型:解答題
如圖,拋物線y=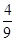 x2-
x2-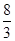 x-12與x軸交于A、C兩點,與y軸交于B點.
x-12與x軸交于A、C兩點,與y軸交于B點.
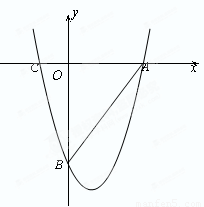
(1)求△AOB的外接圓的面積;
(2)若動點P從點A出發,以每秒2個單位沿射線AC方向運動;同時,點Q從點B出發,以每秒1個單位沿射線BA方向運動,當點P到達點C處時,兩點同時停止運動。問當t為何值時,以A、P、Q為頂點的三角形與△OAB相似?
(3)若M為線段AB上一個動點,過點M作MN平行于y軸交拋物線于點N.
①是否存在這樣的點M,使得四邊形OMNB恰為平行四邊形?若存在,求出點M的坐標;若不存在,請說明理由.
②當點M運動到何處時,四邊形CBNA的面積最大?求出此時點M的坐標及四邊形CBAN面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com