
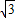 ,∠B為銳角,且關于x的方程x2-4xcosB+1=0有兩個相等的實數根.D是劣弧
,∠B為銳角,且關于x的方程x2-4xcosB+1=0有兩個相等的實數根.D是劣弧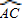 上任一點(點D不與點A、C重合),DE平分∠ADC,交⊙O于點E,交AC于點F.
上任一點(點D不與點A、C重合),DE平分∠ADC,交⊙O于點E,交AC于點F.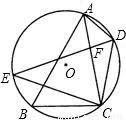
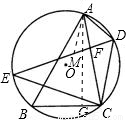
 ;
; BC•AG=6
BC•AG=6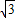 ,
,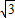 ÷4=3
÷4=3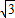 ;
;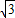 ,則BG=3;
,則BG=3;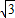 ,由勾股定理,得:
,由勾股定理,得: =2
=2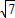 ;
;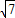 ;
;

 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:初中數學 來源:2002年全國中考數學試題匯編《二次函數》(05)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2002年全國中考數學試題匯編《反比例函數》(01)(解析版) 題型:選擇題
查看答案和解析>>
科目:初中數學 來源:2010年中考數學模擬卷(1)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2002年黑龍江省哈爾濱市中考數學試卷(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2002年黑龍江省哈爾濱市中考數學試卷(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com