【題目】某商場銷售A、B兩種品牌的洗衣機,進價及售價如下表：
(1)該商場9月份用45000元購進A、B兩種品牌的洗衣機，全部售完后獲利9600元，求商場9月份購進A、B兩種洗衣機的數量；
(2)該商場10月份又購進A、B兩種品牌的洗衣機共用去36000元，
①問該商場共有幾種進貨方案?請你把所有方案列出來.
②通過計算說明洗衣機全部銷售完后哪種進貨方案所獲得的利潤最大.
【答案】（1）A品牌購進12臺，B品牌購進15臺；（2）①有三種，方案一：A品牌6臺，B品牌15臺；方案二：A品牌12臺，B品牌10臺；方案三：A品牌18臺，B品牌5臺；②方案一：A品牌6臺，B品牌15臺的利潤最大，理由見解析
【解析】
（1）設A品牌購進
臺，B品牌購進y臺，根據總進價45000元和利潤9600元列方程組求出x、y的值即可得答案；
（2）①根據總進價36000元得出關于a、b的二元一次方程，根據a、b為正整數求出方程的解即可；
②分別求出三種方案的利潤，即可得答案.
(1)設A品牌購進臺，B品牌購進y臺，
∵商場9月份用45000元購進A、B兩種品牌的洗衣機，全部售完后獲利9600元，
∴
，
解得：
.
答：A品牌購進12臺，B品牌購進15臺.
(2)①設A品牌購進
臺，B品牌購進
臺，
∵購進A、B兩種品牌的洗衣機共用去36000元，
∴
∴
∵a、b為正整數，
∴方程的解為
，
，
，
∴購買方案有三種，
方案一：
品牌6臺，
品牌15臺；
方案二：品牌12臺，品牌10臺；
方案三：品牌18臺，品牌5臺.
②方案一利潤：
，
方案二利潤：
，
方案三利潤：
，
∵
∴方案一利潤最大.
閱讀快車系列答案科目：初中數學 來源： 題型：
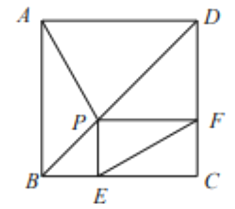
【題目】如圖，己知正方形ABCD的邊長為4, P是對角線BD上一點，PE⊥BC于點E, PF⊥CD于點F,連接AP, EF.給出下列結論:①PD=
EC:②四邊形PECF的周長為8;③△APD一定是等腰三角形:④AP=EF；⑤EF的最小值為
；⑥AP⊥EF.其中正確結論的序號為（ ）
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
查看答案和解析>>
科目：初中數學 來源： 題型：
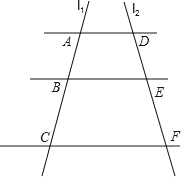
【題目】如圖，已知AD∥BE∥CF，它們以此交直線l1、l2于點A、B、C和D、E、F．若
，AC=14，
（1）求AB的長．
（2）如果AD=7，CF=14，求BE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，已知一次函數
的圖象與
軸，
軸分別交于點
，
.以
為邊在第一象限內作等腰
，且
，
.過
作
軸于點
.
的垂直平分線
交于點
，交軸于點
.
（1）求點的坐標；
（2）連接
，判定四邊形
的形狀，并說明理由；
（3）在直線上有一點
，使得
，求點的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在今年我市初中學業水平考試體育學科的女子800米耐力測試中，某考點同時起跑的小瑩和小梅所跑的路程S（米）與所用時間t（秒）之間的函數圖象分別為線段OA和折線OBCD，下列說法正確的是（ ）
A、小瑩的速度隨時間的增大而增大B、小梅的平均速度比小瑩的平均速度大
C、在起跑后180秒時，兩人相遇D、在起跑后50秒時，小梅在小瑩的前面
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，∠BAD＝44°，AB的垂直平分線交對角線AC于點F，垂足為E，連結DF，則∠CDF等于( )
A. 112°B. 114°C. 116°D. 118°
查看答案和解析>>
科目：初中數學 來源： 題型：
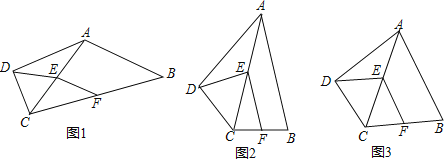
【題目】如圖1，在四邊形ABCD中，∠ADC＝90°，AB＝AC．點E、F分別為AC、BC的中點，連結EF、DE．
（1）請在圖1中找出長度相等的兩條線段？并說明理由．（AB＝AC除外）
（2）如圖2，當AC平分∠BAD，∠DEF＝90°時，求∠BAD的度數．
（3）如圖3，四邊形CDEF是邊長為2的菱形，求S四邊形ABCD．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
