
 +1)
+1) +1)
+1) ,由直角三角形的性質可知AE=BE=
,由直角三角形的性質可知AE=BE= ,再根據勾股定理求出x的值,利用梯形的面積公式求解即可.
,再根據勾股定理求出x的值,利用梯形的面積公式求解即可.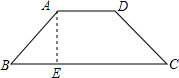 解:如圖所示:梯形ABCD是等腰梯形,AB=10,BC=2AD,∠B=45°
解:如圖所示:梯形ABCD是等腰梯形,AB=10,BC=2AD,∠B=45° ,
, ,
, )2+(
)2+( )2,解得x=10
)2,解得x=10 ,
, ,AD=10
,AD=10 ,AE=5
,AE=5 ,
, (AD+BC)×AE=
(AD+BC)×AE= ×30
×30 ×5
×5 =150.
=150.

 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com