
【題目】某公司為一種新型電子產品在該城市的特約經銷商,已知每件產品的進價為40元,該公司每年銷售這種產品的其他開支(不含進貨價)總計100萬元,在銷售過程中得知,年銷售量y(萬件)與銷售單價x(元)之間存在如表所示的函數關系,并且發現y是x的一次函數.
銷售單價x(元) | 50 | 60 | 70 | 80 |
銷售數量y(萬件) | 5.5 | 5 | 4.5 | 4 |
(1)求y與x的函數關系式;
(2)問:當銷售單價x為何值時,該公司年利潤最大?并求出這個最大值;
【備注:年利潤=年銷售額﹣總進貨價﹣其他開支】
(3)若公司希望年利潤不低于60萬元,請你幫助該公司確定銷售單價的范圍.
【答案】
(1)解:設y=kx+b,把(60,5),(80,4)代入得: ![]() ,
,
解得: 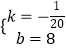 ,
,
故答案為:y=﹣ ![]() x+8;
x+8;
(2)解:該公司年利潤w=(﹣ ![]() x+8)(x﹣40)﹣100=﹣
x+8)(x﹣40)﹣100=﹣ ![]() (x﹣100)2+80,
(x﹣100)2+80,
當x=100時,該公司年利潤最大值為80萬元;
(3)解:由題意得:﹣ ![]() (x﹣100)2+80=60,
(x﹣100)2+80=60,
解得:x1=80,x2=120,
故該公司確定銷售單價x的范圍是:80≤x≤120.
【解析】(1)利用表格,用待定系數法就可以求出y與x的函數關系式;
(2)該公司的年利潤=年銷售數量![]() 單件利潤-公司每年銷售這種產品的其他開支(不含進貨價)總計100萬元,列出函數關系式,并配成頂點式就可以得出結論;
單件利潤-公司每年銷售這種產品的其他開支(不含進貨價)總計100萬元,列出函數關系式,并配成頂點式就可以得出結論;
(3)根據公司希望年利潤不低于60萬元得出方程求解即可得出該公司確定銷售單價的范圍.
【考點精析】本題主要考查了二次函數的最值的相關知識點,需要掌握如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a才能正確解答此題.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:
【題目】某超市預測某飲料會暢銷、先用1800元購進一批這種飲料,面市后果然供不應求,又用8100元購進這種飲料,第二批飲料的數量是第一批的3倍,但單價比第一批貴2元.
(1)第一批飲料進貨單價多少元?
(2)若兩次進飲料都按同一價格銷售,兩批全部售完后,獲利不少于2700元,那么銷售單價至少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y= ![]() +bx+c與x軸交于A(﹣1,0),B(3,0)兩點,與y軸交于C(0,﹣3).
+bx+c與x軸交于A(﹣1,0),B(3,0)兩點,與y軸交于C(0,﹣3).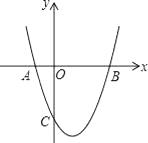
(1)求拋物線的解析式;
(2)D是y軸正半軸上的點,OD=3,在線段BD上任取一點E(不與B,D重合),經過A,B,E三點的圓交直線BC于點F,
①試說明EF是圓的直徑;
②判斷△AEF的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知A(0,a),B(b,0),C(6,c)三點,其中a,b,c滿足關系式|a-2|+(b-3)2+![]() =0,
=0,
(1)求A.B.C的坐標;
(2)求三角形ABC的面積;
(3)在y軸上是否存在點P,使三角形APC的面積與三角形ABC的面積相等?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5![]() cm,點M從點A出發沿折線A﹣B﹣C﹣D運動到點D,且在AB上運動的速度為
cm,點M從點A出發沿折線A﹣B﹣C﹣D運動到點D,且在AB上運動的速度為![]() cm/s,在BC上運動的速度為1cm/s,在CD上運動的速度為
cm/s,在BC上運動的速度為1cm/s,在CD上運動的速度為![]() cm/s,連接AM、DM,當點M運動時間為_____(s)時,△ADM是直角三角形.
cm/s,連接AM、DM,當點M運動時間為_____(s)時,△ADM是直角三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
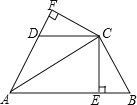
【題目】(本題8分) 已知,如圖,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求證:BE=DF;
(2)若AB=5,AD=3,求AE的長;
(3)若△ABC的面積是23,△ADC面積是18,則△BEC的面積等于 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某種車的耗油量,我們對這種車在高速公路以100km/h的速度做了耗油試驗,并把試驗的數據記錄下來,制成下表:
汽車行駛時間t(h) | 0 | 1 | 2 | 3 | … | |
油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
(1)根據上表的數據,你能用t表示Q嗎?試一試;
(2)汽車行駛6h后,油箱中的剩余油量是多少?
(3)若汽車油箱中剩余油量為52L,則汽車行駛了多少小時?
(4)若該種汽車油箱只裝了36L汽油,汽車以100km/h的速度在一條全長700公里的高速公路上勻速行駛,請問它在中途不加油的情況下能從高速公路起點開到高速公路終點嗎,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是8×8的正方形網格,每個小方格都是邊長為1的正方形,A、B是格點(網格線的交點).以網格線所在直線為坐標軸,在網格中建立平面直角坐標系xOy,使點A坐標為(﹣2,4).
(1)在網格中,畫出這個平面直角坐標系;
(2)在第二象限內的格點上找到一點C,使A、B、C三點組成以AB為底邊的等腰三角形,且腰長是無理數,則點C的坐標是 ;并畫出△ABC關于y軸對稱的△A′B′C′.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com