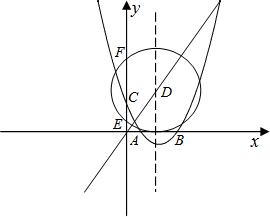
(1)①解:連接AM,過M作MQ⊥x軸于Q,
則AQ=4-1=3,MQ=4,
由勾股定理得:AM=
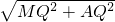
=5,
把M(4,4)代入y=-

x+b得:4=-

×4+b,
∴b=7,
故答案為:5,7.
②解:相切,
理由是:連接AF,
y=-

x+7,
當x=0時,y=7,∴C(0,7),OC=7,
當y=0時,0=-

x+7,
∴x=

,
∴B(

,0),OB=

,
∴BQ=OB-OQ=

-4=

,AQ=4-1=3,MQ=4,
∴
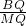
=
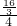
=

,
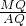
=

,
∴
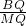
=
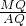
,
∵∠MQA=∠MQB,
∴△AMQ∽△MBQ,
∴∠MAQ=∠BMQ,
∵∠MAQ+∠AMQ=90°,
∴∠AMQ+∠BMQ=90°,
∴AM⊥BC,
∴直線BC與⊙A的位置關系是相切.
(2)解:連接AC,
在△COB中,由勾股定理得:BC=
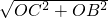
=

,
同理AC=5

,
∵AM=5,由勾股定理得:CM=5,
設EG=a,
∵EF⊥BC,
∴∠FEB=∠COB=90°,
∵∠OBC=∠OBC,
∴△BEG∽△BOC,
∴
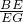
=

,
即

=
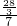
,
∴BE=

a,
∴根據切線長定理得:EM=EF=BC-BE-CM=

-

a-5,
∵EF⊥CB,AF⊥EF,
∴AF∥BC,
∴△AFG∽△BEG,
∴

=

,
∴
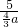
=
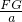
,
∴FG=

,
∵BE+EM+CM=BC,
∴

a+a+

+5=

,
a=

,
EG=

,FG=

,
∴
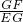
=
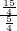
=3.
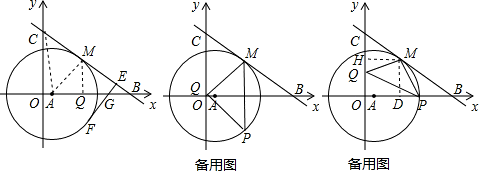
(3)解:①當∠PQM=90°時,MQ=PQ,由對稱性M,P關于X軸對稱,
所以Q,O重合,Q(0,0);
②當∠PMQ=90°,MQ=MP,作MD⊥x,MH⊥y,
可得△MHQ≌△MDP,
即P是圓與x正半軸交點
從而Q(0,2);
③當∠QPM=90°時,分兩種情況:
第一情況:P在y的左方,如圖,設P(m,n),Q(0,b)可得:
①4-m=n-b,②4-n=-m,③(1-m)
2+n
2=5
2,
解方程組得,b=2,b=-8(b=2也符合條件,雖與②中b同,但直角不同),
第二情況:P在y的右方,同理得:

①m-4=n-b,②4-n=m,③(1-m)
2+n
2=5
2,
解方程組得,b=3+

(舍),b=3-

.
綜合上述:Q的坐標是(0,0)或(0,2)或(0,-8)或(0,3-

).
分析:(1)①連接AM,過M作MQ⊥x軸于Q,求出AQ、QM,根據勾股定理求出AM即可;把M的坐標代入解析式,求出b即可;②求出B、C的坐標,證△AQM和△BQM相似,推出∠MAQ=∠BMQ,推出∠AMB=90°即可;
(2)設EG=a,根據勾股定理求出BC、AC、CM的值,根據△BEG和△BOC相似,求出BE的值,根據△BEG和△AFG相似,求出GF的值,根據BC=BE+EM+CM,代入求出a即可;
(3)有三種情況:①當∠PQM=90°時,MQ=PQ,根據軸對稱,得出Q與O重合,即可求出Q的坐標;②當∠PMQ=90°,MQ=MP,作MD⊥x,MH⊥y,證△MHQ≌△MDP,推出P是圓與x正半軸交點,即可求出答案;③當∠QPM=90°時,分兩種情況:第一情況:P在y的左方,設P(m,n),Q(0,b)得出方程①4-m=n-b,②4-n=-m,③(1-m)
2+n
2=5
2,解方程組即可求出b;第二情況:P在y的右方,同理能求出b的值.
點評:本題綜合考查了勾股定理,等腰三角形性質,等腰直角三角形,切線的判定,相似三角形的性質和判定,軸對稱性質,切線長定理,直線與圓的位置關系等知識點,主要考查學生綜合運用性質進行推理和計算能力,本題難度偏大,對學生提出了較高的要求,用力方程思想和分類討論思想.

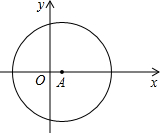 直角坐標系中,已知A(1,0),以點A為圓心畫圓,點M(4,4)在⊙A上,直線y=-
直角坐標系中,已知A(1,0),以點A為圓心畫圓,點M(4,4)在⊙A上,直線y=- x+b過點M,分別交x軸、y軸于B、C兩點.
x+b過點M,分別交x軸、y軸于B、C兩點.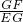 的值.
的值.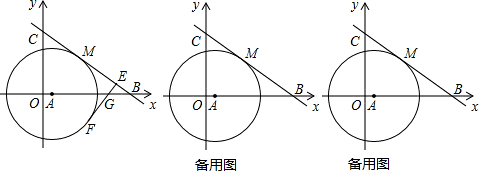
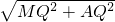 =5,
=5, x+b得:4=-
x+b得:4=- ×4+b,
×4+b,
 x+7,
x+7, x+7,
x+7, ,
, ,0),OB=
,0),OB= ,
, -4=
-4= ,AQ=4-1=3,MQ=4,
,AQ=4-1=3,MQ=4,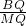 =
=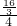 =
= ,
,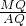 =
= ,
,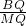 =
=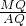 ,
,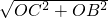 =
= ,
, ,
,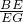 =
= ,
, =
=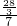 ,
, a,
a, -
- a-5,
a-5, =
= ,
,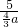 =
=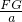 ,
, ,
, a+a+
a+a+ +5=
+5= ,
, ,
, ,FG=
,FG= ,
,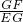 =
=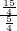 =3.
=3.
 (舍),b=3-
(舍),b=3- .
. ).
).

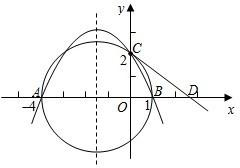 軸的正半軸于點C(0,2),過點C作圓的切線交x軸于點D.
軸的正半軸于點C(0,2),過點C作圓的切線交x軸于點D.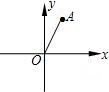 如圖,在直角坐標系中,已知點A(1,
如圖,在直角坐標系中,已知點A(1,