
【題目】我國古代數學名著《九章算術》的論割圓術中有:“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣.”它體現了一種無限與有限的轉化過程.比如在表達式1+ ![]() 中“”即代表無數次重復,但原式卻是個定值,它可以通過方程1+
中“”即代表無數次重復,但原式卻是個定值,它可以通過方程1+ ![]() =x求得x=
=x求得x= ![]() .類比上述過程,則
.類比上述過程,則 ![]() =( )
=( )
A.3
B.![]()
C.6
D.2 ![]()
 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上且以4為周期的奇函數,當x∈(0,2)時,f(x)=ln(x2﹣x+b),若函數f(x)在區間[﹣2,2]上的零點個數為5,則實數b的取值范圍是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正實數a,b滿足:a+b=2.
(1)求 ![]() 的最小值m;
的最小值m;
(2)設函數f(x)=|x﹣t|+|x+ ![]() |(t≠0),對于(Ⅰ)中求得的m,是否存在實數x,使得f(x)=m成立,若存在,求出x的取值范圍,若不存在,說明理由.
|(t≠0),對于(Ⅰ)中求得的m,是否存在實數x,使得f(x)=m成立,若存在,求出x的取值范圍,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知D,E是△ABC邊BC的三等分點,點P在線段DE上,若 ![]() =x
=x ![]() +y
+y ![]() ,則xy的取值范圍是( )
,則xy的取值范圍是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在以A,B,C,D,E,F為頂點的多面體中,四邊形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2 ![]() .
. 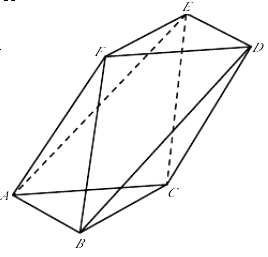
(1)求證:平面ABC⊥平面ACDF;
(2)求平面AEF與平面ACE所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分別為棱AA1 , AC的中點. 
(1)在平面ABC內過點A作AM∥平面PQB1交BC于點M,并寫出作圖步驟,但不要求證明;
(2)若側面ACC1A1⊥側面ABB1A1 , 求直線A1C1與平面PQB1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線 ![]() (t為參數)恒過橢圓
(t為參數)恒過橢圓 ![]() (φ為參數)在右焦點F.
(φ為參數)在右焦點F.
(1)求m的值;
(2)設直線l與橢圓C交于A,B兩點,求|FA||FB|的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2lnx+x2+(a﹣1)x﹣a,(a∈R),當x≥1時,f(x)≥0恒成立.
(1)求實數a的取值范圍;
(2)若正實數x1、x2(x1≠x2)滿足f(x1)+f(x2)=0,證明:x1+x2>2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com