
【題目】我們定義:如圖1,在△ABC中,把AB繞點A按順時針方向旋轉α(0°<α<180°)得到AB′,把AC繞點A按逆時針方向旋轉β得到AC′,連接B′C′,當α+β=180°時,我們稱△AB′C′是△ABC的“旋補三角形”,△AB′C′邊B′C′上的中線AD叫做△ABC的“旋補中線”,點A叫做“旋補中心”.
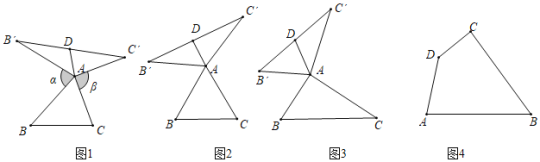
(1)特例感知:在圖2、圖3中,△AB′C′是△ABC的“旋補三角形”,AD是△ABC的“旋補中線”.
①如圖2,當△ABC為等邊三角形時,AD與BC的數量關系為AD=______BC;
②如圖3,當∠BAC=90°,BC=8時,則AD長為______.
(2)精確作圖:如圖4,已知在四邊形ABCD內部存在點P,使得△PDC是△PAB的“旋補三角形”(點D的對應點為點A,點C的對應點為點B),請用直尺和圓規作出點P(要求:保留作圖痕跡,不寫作法和證明)
(3)猜想論證:在圖1中,當△ABC為任意三角形時,猜想AD與BC的數量關系,并給予證明.
【答案】(1)①![]() ,②4;(2)見解析;(3)AD=
,②4;(2)見解析;(3)AD=![]() BC.
BC.
【解析】
(1)①根據含30°直角三角形的性質解答;②證明△AB′C′≌△ABC,根據全等三角形的性質得到B′C′=BC,根據直角三角形的性質計算;
(2)根據線段垂直平分線的性質、利用尺規作圖作出點P;
(3)證明四邊形AB′EC′是平行四邊形,得到B′E=AC′,∠B′AC′+∠AB′E=180°,根據全等三角形的性質得到AE=BC,得到答案.
解:(1)①∵△ABC是等邊三角形,
∴AB=AC=BC,∠BAC=60°,
∵△AB′C′是△ABC的“旋補三角形”,
∴∠B′AC′=120°,AB=AB′,AC=AC′,
∴AB′=AC′,
∴∠AB′D=30°,
∴AD=![]() AB′,
AB′,
∴AD=![]() BC,
BC,
故答案為:![]() ;
;
②∵△AB′C′是△ABC的“旋補三角形”,
∴∠B′AC′=∠BAC=90°,AB=AB′,AC=AC′,
在△AB′C′和△ABC中,
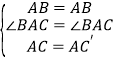 ,
,
∴△AB′C′≌△ABC(SAS)
∴B′C′=BC=8,
∵∠B′AC′=90°,AD是△ABC的“旋補中線”,
∴AD=![]() B′C′=4,
B′C′=4,
故答案為:4;
(2)如圖4,作線段AD、BC的垂直平分線,交點即為點P,

∴點P即為所作;
(3)AD=![]() BC,
BC,
證明:如圖1,延長AD到E,使得DE=AD,連接B′E、C′E,
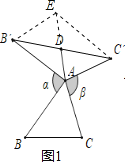
∵AD是△AB′C’的中線,
∴B′D=C′D,
∵DE=AD,
∴四邊形AB′EC′是平行四邊形,
∴B′E=AC′,∠B′AC′+∠AB′E=180°,
∵α+β=180°,
∴∠B′AC′+∠BAC=180°,
∴∠EB′A=∠BAC,
在△EB′A和△CAB中,
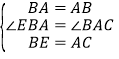
∴△EB′A≌△CAB(SAS),
∴AE=BC,
∴AD=![]() BC.
BC.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
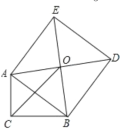
【題目】已知在Rt△ABC中,∠C=90°,以斜邊AB為邊向外作正方形ABDE,且正方形對角線交于點O,連接OC,已知AC=4![]() ,OC=7,則另一條直角邊BC的長為_____.
,OC=7,則另一條直角邊BC的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
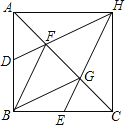
【題目】已知:如圖,在△ABC中,AB=BC,∠ABC=90°,點D、E分別是邊AB、BC的中點,點F、G是邊AC的三等分點,DF、EG的延長線相交于點H,連接HA、HC.
(1)求證:四邊形FBGH是菱形;
(2)求證:四邊形ABCH是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形網格中(網格中的每個小正方形邊長是1),△ABC的頂點均在格點上,請在所給的直角坐標系中解答下列問題:
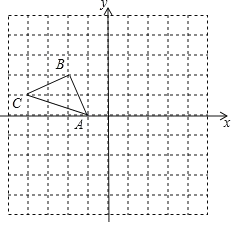
(1)作出△ABC繞點A逆時針旋轉90°的△AB1C1,再作出△AB1C1關于原點O成中心對稱的△A1B2C2.
(2)點B1的坐標為 ,點C2的坐標為 .
(3)請直接寫出以A1、B2、C2為頂點的平行四邊形的第四個頂點D的坐標:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 內并排
內并排![]() 不重疊
不重疊![]() 放入邊長為1的小正方形紙片,第一層小紙片的一條邊都在AB上,首尾兩個正方形各有一個頂點分別在AC、BC上,依次這樣擺放上去,則最多能擺放
放入邊長為1的小正方形紙片,第一層小紙片的一條邊都在AB上,首尾兩個正方形各有一個頂點分別在AC、BC上,依次這樣擺放上去,則最多能擺放![]()
![]() 個小正方形紙片.
個小正方形紙片.
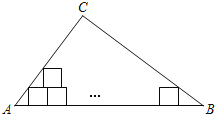
A. 14個 B. 15個 C. 16個 D. 17個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中有點A(0,1)、B(![]() ,0).
,0).
連接AB,以A為圓心,以AB為半徑畫弧,交y軸于點P1;
連接BP1,以B為圓心,以BP1為半徑畫弧,交x軸于點P2;
連接P1P2,以P1為圓心,以P1P2為半徑畫弧,交y軸于點P3;
按照這樣的方式不斷在坐標軸上確定點Pn的位置,那么點P6的坐標是_____.
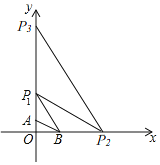
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若該方程有兩個實數根,求m的最小整數值;
(2)若方程的兩個實數根為x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
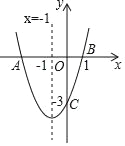
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A、B兩點,與y軸交于點C,對稱軸為直線x=﹣1,點B的坐標為(1,0),則下列結論:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正確的結論有( )個.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com