
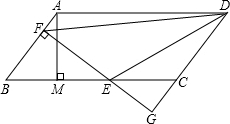
 如圖,平行四邊形ABCD中,AB=5,BC=10,BC邊上的高AM=4,E為BC邊上的一個動點(不與B、C重合),過E作直線AB的垂線,垂足為F,FE與DC的延長線相交于點G,連接DE、DF.有下面三個結論:
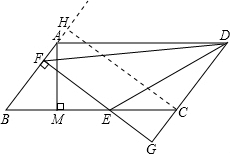
如圖,平行四邊形ABCD中,AB=5,BC=10,BC邊上的高AM=4,E為BC邊上的一個動點(不與B、C重合),過E作直線AB的垂線,垂足為F,FE與DC的延長線相交于點G,連接DE、DF.有下面三個結論: 時,△DEF的面積為
時,△DEF的面積為 ,
,
 =
=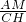
 x,GC=
x,GC= (10-x),
(10-x), EF•DG=
EF•DG= •
• x[
x[ (10-x)+5]=-
(10-x)+5]=-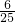 x2+
x2+ x,
x,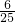 (x-
(x-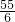 )2+
)2+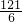 .
.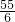 時,y有最大值.
時,y有最大值.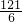 ,故此選項正確.
,故此選項正確. (x+y)=24.
(x+y)=24. x,CG=
x,CG= (10-x),那么利用三角形的面積公式,可得到y與x的關系式,再根據二次函數求最大值來求即可.
(10-x),那么利用三角形的面積公式,可得到y與x的關系式,再根據二次函數求最大值來求即可.

 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:
 次方程x2-7x+12=0的兩個根,且OA>OB.
次方程x2-7x+12=0的兩個根,且OA>OB.| OA |
| AB |
| 16 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 5 |


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com