
【題目】(1)如圖 ,∠AOB=∠COD=90°
①∠AOD=30°求∠BOC
②若∠AOD=α求用α的代數(shù)式表示∠BOC.

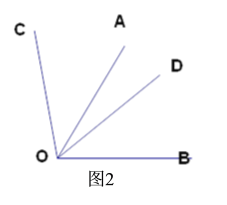
(2)如圖2,若∠AOB=∠COD=60°,直接寫出∠AOC與∠BOD的關系.
【答案】(1)①150°;②180°-α;(2)∠AOC=∠BOD.
【解析】
(1)①根據(jù)∠AOB=∠COD=90°,∠AOD=30°,∠AOC =∠COD-∠AOD=60°,進而求出∠BOC;
②根據(jù)∠AOB=∠COD=90°,∠AOD=α,∠AOC =∠COD-∠AOD=90°-α,進而求出∠BOC;;
(2)將∠AOB=∠COD=60°,寫成∠AOD+∠BOD=∠AOD+∠AOC=60°,即可得出結論.
(1)①∵∠AOB=∠COD=90°,∠AOD=30°,
∴∠BOC=∠AOB+∠AOC
=∠AOB+(∠COD-∠AOD)
=90°+(90°-30°)
=150°;
②∵∠AOB=∠COD=90°,∠AOD=α,
∴∠BOC=∠AOB+∠AOC
=∠AOB+(∠COD-∠AOD)
=90°+(90°-α)
=180°-α;
(2)∠AOC=∠BOC,理由是:
∵∠AOB=∠COD=60°,
∴∠AOD+∠BOD=∠AOD+∠AOC,
∴∠AOC=∠BOD.


 考前必練系列答案
考前必練系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABOC的頂點O在坐標原點,邊BO在x軸的負半軸上,![]() ,頂點C的坐標為
,頂點C的坐標為![]() ,x反比例函數(shù)
,x反比例函數(shù)![]() 的圖象與菱形對角線AO交于點D,連接BD,當
的圖象與菱形對角線AO交于點D,連接BD,當![]() 軸時,k的值是______.
軸時,k的值是______.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某中學決定在本校學生中開展足球、籃球、羽毛球、乒乓球四種活動,為了了解學生對這四種活動的喜愛情況,學校隨機調查了該校m名學生,看他們喜愛哪一種活動(每名學生必選一種且只能從這四種活動中選擇一種),現(xiàn)將調查的結果繪制成如下不完整的統(tǒng)計圖.請你根據(jù)圖中的信息,解答下列問題.
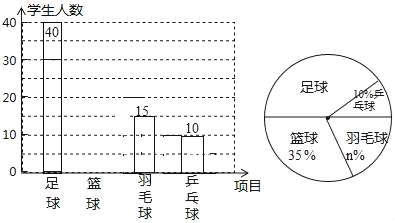
(1)m= ,n= ;
(2)請補全圖中的條形圖;
(3)扇形統(tǒng)計圖中,足球部分的圓心角是 度;
(4)根據(jù)抽樣調查的結果,請估算全校1800名學生中,大約有多少人喜愛踢足球.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
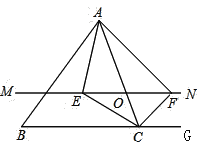
【題目】如圖,在![]() 中,點
中,點![]() 是
是![]() 邊上的一個動點,過點
邊上的一個動點,過點![]() 作直線
作直線![]() ,設
,設![]() 交
交![]() 的角平分線于點
的角平分線于點![]() ,交
,交![]() 的外角平分線于點
的外角平分線于點![]() .
.
(1)求證:![]() ;
;
(2)當點![]() 運動到何處時,四邊形
運動到何處時,四邊形![]() 是矩形?并證明你的結論.
是矩形?并證明你的結論.
(3)當點![]() 運動到何處,且
運動到何處,且![]() 滿足什么條件時,四邊形
滿足什么條件時,四邊形![]() 是正方形?并說明理由.
是正方形?并說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】隨著通訊技術的迅猛發(fā)展,人與人之間的溝通方式更多樣、便捷.某校數(shù)學興趣小組設計了“你最喜歡的溝通方式”調查問卷(每人必選且只選一種),在全校范圍內隨機調查了部分學生,將統(tǒng)計結果繪制了如下兩幅不完整的統(tǒng)計圖,請結合圖中所給的信息解答下列問題:

(1)這次統(tǒng)計共抽查了 名學生;在扇形統(tǒng)計圖中,表示“QQ”的扇形圓心角的度數(shù)為 ;
(2)將條形統(tǒng)計圖補充完整;
(3)該校共有1500名學生,請估計該校最喜歡用“微信”進行溝通的學生有多少名?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,鐵路MN和公路PQ在點O處交匯,∠QON=30°.公路PQ上A處距O點240米.如果火車行駛時,周圍200米以內會受到噪音的影響.那么火車在鐵路MN上沿ON方向以20米/秒的速度行駛時,A處受噪音影響的時間為( )

A. 16秒B. 18秒C. 20秒D. 22秒
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,方格中小正方形的邊長為1,△ABC的三個頂點都在小正方形的格點上,求:
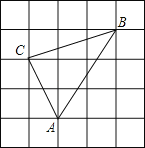
(1)△ABC的周長;
(2)請判斷三角形ABC是否是直角三角形,并說明理由;
(3)△ABC的面積;
(4)點C到AB邊的距離.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】“龜兔首次賽跑”之后,輸了比賽的兔子沒有氣餒,總結反思后,和烏龜約定再賽一場.圖中的函數(shù)圖象刻畫了“龜兔再次賽跑”的故事(x表示烏龜從起點出發(fā)所行的時間,y1表示烏龜所行的路程,y2表示兔子所行的路程).有下列說法:

①“龜兔再次賽跑”的路程為1000米;
②兔子和烏龜同時從起點出發(fā);
③烏龜在途中休息了10分鐘;
④兔子在途中750米處追上烏龜.
其中正確的說法是 .(把你認為正確說法的序號都填上)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在一張三角形紙片ABC中,AB=10cm,BC=7cm,AC=6cm,沿過點B的直線折疊這個三角形,使頂點C落在邊AB上的點E處,折痕為BD.

(1)求△AED的周長.
(2)說明BD垂直平分EC.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com