
 .即
.即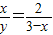 .
. x(3-x)=-
x(3-x)=- x2+
x2+ x(0<x<3).
x(0<x<3). 時,y有最大值
時,y有最大值 ;
;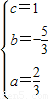
 x2-
x2- x+1;
x+1;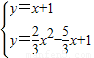 得
得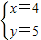 ,
,

 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:
| 1 | 2 |
 O1A1B1C1與矩形OABC的重疊部分的面積是否發生變化?若不變,求出該重疊部分的面積;若改變,請說明理由.
O1A1B1C1與矩形OABC的重疊部分的面積是否發生變化?若不變,求出該重疊部分的面積;若改變,請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |


查看答案和解析>>
科目:初中數學 來源: 題型:
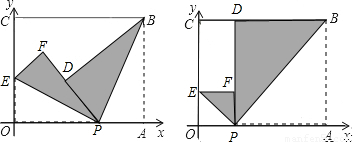
 (2011•鄭州模擬)如圖所示,四邊形OABC是矩形,點A,C的坐標分別為(3,0),(0,l),點D是線段BC上的動點(與端點B,C不重合),過點D作直線y=-
(2011•鄭州模擬)如圖所示,四邊形OABC是矩形,點A,C的坐標分別為(3,0),(0,l),點D是線段BC上的動點(與端點B,C不重合),過點D作直線y=-| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 端點B、C不重合),過點D作直線y=-
端點B、C不重合),過點D作直線y=-| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•吳中區一模)如圖所示,四邊形OABC是矩形,點A、C的坐標分別為(6,0),(0,2),點D是線段BC上的動點(與端點B、C不重合),過點D作直線y=-
(2013•吳中區一模)如圖所示,四邊形OABC是矩形,點A、C的坐標分別為(6,0),(0,2),點D是線段BC上的動點(與端點B、C不重合),過點D作直線y=-| 1 | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com