
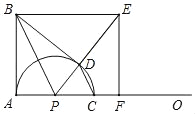
【題目】如圖,∠BAO=90°,AB=8,動點P在射線AO上,以PA為半徑的半圓P交射線AO于另一點C,CD∥BP交半圓P于另一點D,BE∥AO交射線PD于點E,EF⊥AO于點F,連接BD,設AP=m.
(1)求證:∠BDP=90°.
(2)若m=4,求BE的長.
(3)在點P的整個運動過程中.
①當AF=3CF時,求出所有符合條件的m的值.
②當tan∠DBE=![]() 時,直接寫出△CDP與△BDP面積比.
時,直接寫出△CDP與△BDP面積比.
【答案】(1)詳見解析;(2)![]() 的長為10;(3)m的值為
的長為10;(3)m的值為![]() 或
或![]() ;
;![]() 與
與![]() 面積比為
面積比為![]() 或
或![]() .
.
【解析】
![]() 由
由![]() 知
知![]() ,再由
,再由![]() 知
知![]() 、
、![]() ,據此可得
,據此可得![]() ,證
,證![]() ≌
≌![]() 即可得;
即可得;![]() 易知四邊形ABEF是矩形,設
易知四邊形ABEF是矩形,設![]() ,可得
,可得![]() ,證
,證![]() ≌
≌![]() 得
得![]() ,在
,在![]() 中,由
中,由![]() ,列方程求解可得答案;
,列方程求解可得答案;![]() 分點C在AF的左側和右側兩種情況求解:左側時由
分點C在AF的左側和右側兩種情況求解:左側時由![]() 知
知![]() 、
、![]() 、
、![]() ,在
,在![]() 中,由
中,由![]() 可得關于m的方程,解之可得;右側時,由
可得關于m的方程,解之可得;右側時,由![]() 知
知![]() 、
、![]() 、
、![]() ,利用勾股定理求解可得.
,利用勾股定理求解可得.![]() 作
作![]() 于點G,延長GD交BE于點H,由
于點G,延長GD交BE于點H,由![]() ≌
≌![]() 知
知![]() ,據此可得
,據此可得 ,再分點D在矩形內部和外部的情況求解可得.
,再分點D在矩形內部和外部的情況求解可得.
![]() 如圖1,
如圖1,

![]() ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四邊形ABEF是矩形,
四邊形ABEF是矩形,
設![]() ,則
,則![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() 的長為10.
的長為10.
![]() 如圖1,當點C在AF的左側時,
如圖1,當點C在AF的左側時,
![]() ,則
,則![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 負值舍去
負值舍去![]() ;
;
如圖2,當點C在AF的右側時,

![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 負值舍去
負值舍去![]() ;
;
綜上,m的值為![]() 或
或![]() ;
;
![]() 如圖3,過點D作
如圖3,過點D作![]() 于點G,延長GD交BE于點H,
于點G,延長GD交BE于點H,

![]() ≌
≌![]() ,
,
![]() ,
,
又![]() ,且
,且![]() ,
,
 ,
,
當點D在矩形ABEF的內部時,
由![]() 可設
可設![]() 、
、![]() ,
,
則![]() ,
,
![]() ,
,
則![]() ;
;
如圖4,當點D在矩形ABEF的外部時,

由![]() 可設
可設![]() 、
、![]() ,
,
則![]() ,
,
![]() ,
,
則![]() ,
,
綜上,![]() 與
與![]() 面積比為
面積比為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】因商人、商業、商品發源于商丘,商朝建都于河南商丘,商丘被譽為“三商之源,華商之都”![]() 商字是商丘市的城市地標,坐落在河南省商丘市睢陽區神火大道與南京路交匯處中的環島內,雕塑建成與1997年6月29日,某中學九年級數學興趣小組想測量商字雕塑AB的高度,小明在雕塑前一座寫字樓CD分E處仰望商字雕塑的頂端A,測得仰角為
商字是商丘市的城市地標,坐落在河南省商丘市睢陽區神火大道與南京路交匯處中的環島內,雕塑建成與1997年6月29日,某中學九年級數學興趣小組想測量商字雕塑AB的高度,小明在雕塑前一座寫字樓CD分E處仰望商字雕塑的頂端A,測得仰角為![]() ,小亮在寫字樓前F處,測得商字雕塑的頂端A的仰角為
,小亮在寫字樓前F處,測得商字雕塑的頂端A的仰角為![]() ,有裝B,F,D在同一條直線上,
,有裝B,F,D在同一條直線上,![]() ,
,![]() ,求商字雕塑AB的高度
,求商字雕塑AB的高度![]() 測角器的高度忽略不計,結果精確到1米
測角器的高度忽略不計,結果精確到1米![]() 參考數據:
參考數據:![]() ,
,![]() ,
,![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求證:AD平分∠BAC;
(2)直接寫出AB+AC與AE之間的等量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD和正方形EFGH的中心重合,![]() ,
,![]() ,
,![]() 分別延長FE,GF,HG和EH交AB,BC,CD,AD于點I,J,K,
分別延長FE,GF,HG和EH交AB,BC,CD,AD于點I,J,K,![]() 若
若![]() ,則AI的長為______,四邊形AIEL的面積為______.
,則AI的長為______,四邊形AIEL的面積為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知函數![]() 的圖象與x軸、y軸分別交于點A,B,與函數y=x的圖象交于點M,點M的橫坐標為2.在x軸上有一點P (a,0)(其中a>2),過點P作x軸的垂線,分別交函數
的圖象與x軸、y軸分別交于點A,B,與函數y=x的圖象交于點M,點M的橫坐標為2.在x軸上有一點P (a,0)(其中a>2),過點P作x軸的垂線,分別交函數![]() 和y=x的圖象于點C,D.
和y=x的圖象于點C,D.
(1)求點A的坐標;
(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀理解下面的例題,再按要求解答下列問題:
例題:解一元二次不等式,![]()
解:∵![]() ,∴
,∴![]() 可化為,
可化為,![]()
由有理數的乘法法則“兩數相乘,同號得正”,有
(1)![]() 或(2)
或(2)![]()
解不等式組(1),得![]() ,解不等式組(2),得
,解不等式組(2),得![]() ,
,
故![]() 的解集為
的解集為![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集為
的解集為![]() 或
或![]() .
.
問題:(1)一元二次不等式![]() 的解集為______.
的解集為______.
(2)求分式不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們在學習“實數”時畫了這樣一個圖,即“以數軸上的單位長為‘1’的線段作一個正方形,然后以原點O為圓心,正方形的對角線長為半徑畫弧交數軸于點A”,請根據圖形回答下列問題:
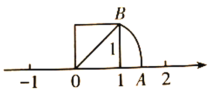
(1)線段OA的長度是多少?(要求寫出求解過程)
(2)這個圖形的目的是為了說明什么?
(3)這種研究和解決問題的方式體現了 的數學思想方法.(將下列符合的選項序號填在橫線上)
A.數形結合 B.代入 C.換元 D.歸納
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣![]() x2﹣
x2﹣![]() x+2與x軸交于A、B兩點,與y軸交于點C
x+2與x軸交于A、B兩點,與y軸交于點C
(1)求點A,B,C的坐標;
(2)點E是此拋物線上的點,點F是其對稱軸上的點,求以A,B,E,F為頂點的平行四邊形的面積;
(3)此拋物線的對稱軸上是否存在點M,使得△ACM是等腰三角形?若存在,請求出點M的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com