
【題目】如圖,一次函數y=kx+2的圖象與反比例函數y= ![]() 的圖象交于P、G兩點,過點P作PA⊥x軸,一次函數圖象分別交x軸、y軸于C、D兩點,
的圖象交于P、G兩點,過點P作PA⊥x軸,一次函數圖象分別交x軸、y軸于C、D兩點, ![]() =
= ![]() ,且S△ADP=6.
,且S△ADP=6. 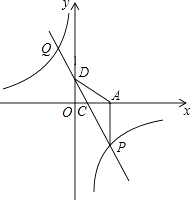
(1)求點D坐標;
(2)求一次函數和反比例函數的表達式;
(3)根據圖象直接寫出一次函數值小于反比例函數值時,自變量x的取值范圍.
【答案】
(1)解:對于y=kx+2,令x=0,得到y=2,即D(0,2)
(2)解:∵AP∥y軸,∴ ![]() =
= ![]() =
= ![]() ,
,
∵OD=2,∴AP=4,
∵S△ADP= ![]() APOA=6,
APOA=6,
∴OA=3,即P(3,﹣4),
把P坐標代入反比例解析式得:m=﹣12,
∴反比例函數解析式為y=﹣ ![]() ,
,
把P坐標代入y=kx+2中得:﹣4=3k+2,即k=﹣2,
∴一次函數解析式為y=﹣2x+2
(3)解:聯立得: 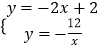 ,
,
解得: ![]() 或
或 ![]() ,
,
∴Q(﹣2,6),P(3,﹣4),
則由圖象得:當x>3或﹣2<x<0時,一次函數值小于反比例函數值
【解析】(1)對于一次函數,令x=0求出y的值,即可確定出D坐標;(2)由AP與y軸平行,得比例,根據OD的長求出AP的長,由三角形ADP面積求出OA的長,確定出P坐標,代入反比例解析式求出m的值,代入一次函數求出k的值,即可確定出各自的解析式;(3)聯立一次函數與反比例函數解析式求出交點坐標,確定出G坐標,利用圖象確定出一次函數值小于反比例函數值時x的范圍即可.


科目:初中數學 來源: 題型:
【題目】閱讀下列材料并回答問題: 材料1:如果一個三角形的三邊長分別為a,b,c,記 ![]() ,那么三角形的面積為
,那么三角形的面積為 ![]() . ①
. ①
古希臘幾何學家海倫(Heron,約公元50年),在數學史上以解決幾何測量問題而聞名.他在《度量》一書中,給出了公式①和它的證明,這一公式稱海倫公式.
我國南宋數學家秦九韶(約1202﹣﹣約1261),曾提出利用三角形的三邊求面積的秦九韶公式: ![]() . ②
. ②
下面我們對公式②進行變形: ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
這說明海倫公式與秦九韶公式實質上是同一公式,所以我們也稱①為海倫﹣﹣秦九韶公式.
問題:如圖,在△ABC中,AB=13,BC=12,AC=7,⊙O內切于△ABC,切點分別是D、E、F.
(1)求△ABC的面積;
(2)求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,O為直線AB上一點,過點O作射線OC,使∠BOC=110°.將一三角尺的直角頂點放在點O處(∠OMN=30°),一邊OM在射線OB上,另一邊ON在直線AB的下方.
(1)將圖①中的三角尺繞點O逆時針旋轉至圖②,使一邊OM在∠BOC的內部,且恰好平分∠BOC,求∠BON的度數;
(2)將圖①中的三角尺繞點O以每秒5°的速度按逆時針方向旋轉一周,在旋轉的過程中,第t秒時,直線ON恰好平分銳角∠AOC,則t的值為________(直接寫出結果);
(3)將圖①中的三角尺繞點O順時針旋轉至圖③,使ON在∠AOC的內部,請探究∠AOM與∠NOC的數量關系,并說明理由.
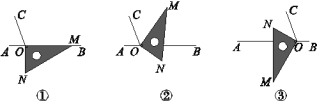
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數-5,1,-3,5,-2中任取三個數相乘,其中最大的積是a,最小的積是b.
(1)求a,b的值;
(2)若|x+a|+|y-b|=0,求(x+y)÷(x-y)的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,并且關于x的一元二次方程ax2+bx+c﹣m=0有兩個不相等的實數根,下列結論: ①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正確的個數有( )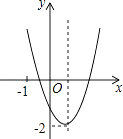
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD繞點C順時針旋轉90°得到矩形FGCE,點M、N分別是BD、GE的中點,若BC=14,CE=2,則MN的長( )

A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某城市市民廣場一入口處有五級高度相等的小臺階.已知臺階總高1.5米,為了安全,現要做一個不銹鋼扶手AB及兩根與FG垂直且長為1米的不銹鋼架桿AD和BC(桿子的底端分別為D、C),且∠DAB=66.5°.(參考數據:cos66.5°≈0.40,sin66.5°≈0.92) 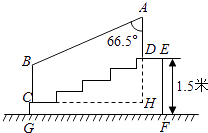
(1)求點D與點C的高度差DH;
(2)求所有不銹鋼材料的總長度(即AD+AB+BC的長,結果精確到0.1米)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD,∠A=60°,AB=4,以點B為圓心的扇形與邊CD相切于點E,扇形的圓心角為60°,點E是CD的中點,圖中兩塊陰影部分的面積分別為S1 , S2 , 則S2﹣S1= . 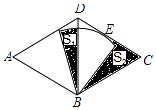
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com