Question

如圖①，在平面直角坐標中，點A的坐標為（1，﹣2），點B的坐標為（3，﹣1），二次函數y=﹣x2的圖象為l1．

（1）平移拋物線l1，使平移后的拋物線經過點A，但不過點B．

①滿足此條件的函數解析式有 個．

②寫出向下平移且經點A的解析式 ．

（2）平移拋物線l1，使平移后的拋物線經過A，B兩點，所得的拋物線l2，如圖②，求拋物線l2的函數解析式及頂點C的坐標，并求△ABC的面積．

（3）在y軸上是否存在點P，使S△ABC=S△ABP？若存在，求出點P的坐標；若不存在，請說明理由．

 

 

Answer 1

（1）①無數；②y=﹣x2﹣1；（2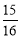）；（3）存在，點P的坐標為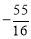（0，）或（0，）．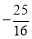

【解析】

試題分析：（1）①根據實際情況可以直接寫出結果．

②設平移以后的二次函數解析式是：y=﹣x2+c，把（1，﹣2）代入即可求得c=﹣1，從而得到函數的解析式：y=﹣x2﹣1．

（2）利用待定系數法即可求得函數的解析式；化為頂點式得到點C 的坐標，過點A、B、C三點分別作x軸的垂線，垂足分別為D、EE、F，求得△ABC的面積．

（3）分當點P位于點G的下方和上方，兩種情況進行討論求解．

試題解析：【解析】
（1）①無數；

②y=﹣x2﹣1．

（2）設l2的解析式是y=x2+bx+c，

∵l2經過點A（1，﹣2）和B（3，﹣1），

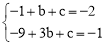∴，解得：．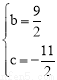

∴l2的解析式是：．

∵，

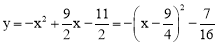∴頂點C的坐標是．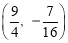

如答圖1，過點A、B、C三點分別作x軸的垂線，垂足分別為D、E、F，

則AD=2，CF=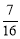，BE=1，DE=2，DF=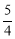，FE=．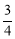

∴S△ABC=S梯形ABED﹣S梯形BCFE﹣S梯形ACFD=．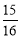

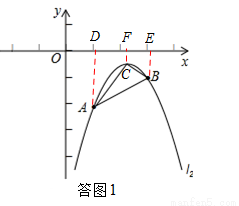
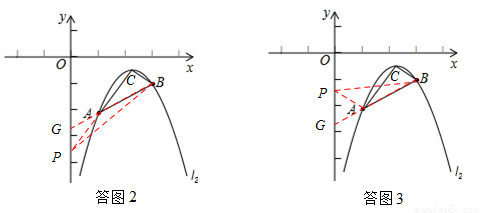
（3）存在．如答圖2，3，延長BA交y軸于點G，

設直線AB的解析式為，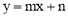

則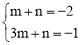，解得．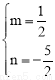

∴直線AB的解析式為．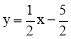

∴點G的坐標為（0，）．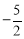

設點P的坐標為（0，h），

①當點P位于點G的下方時，如答圖2，PG=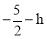，連接AP、BP，

則S△ABP=S△BPG﹣S△APG=．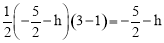

又∵S△ABC=S△ABP=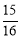，得h=．

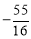∴點P的坐標為（0，）．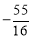

②當點P位于點G的上方時，如答圖3，PG=，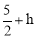

同上可得h=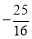，點P的坐標為（0，）．

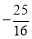綜上所述，所求點P的坐標為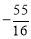（0，）或（0，）．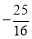

考點：1．二次函數綜合題；2．線動平移問題；3．待定系數法的應用；4．曲線上點的坐標與方程的關系；5．二次函數的性質；6．三角形和梯形面積；7．分類思想、轉換思想和方程思想的應用．