
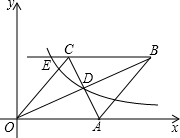
 如圖,已知:如圖,在直角坐標(biāo)系中,有菱形OABC,A點的坐標(biāo)為(10,0),對角線OB、AC相交于D點,雙曲線y=
如圖,已知:如圖,在直角坐標(biāo)系中,有菱形OABC,A點的坐標(biāo)為(10,0),對角線OB、AC相交于D點,雙曲線y= (x>0)經(jīng)過D點,交BC的延長線于E點,且OB•AC=160,有下列四個結(jié)論:
(x>0)經(jīng)過D點,交BC的延長線于E點,且OB•AC=160,有下列四個結(jié)論: (x>0);②E點的坐標(biāo)是(5,8);③sin∠COA=
(x>0);②E點的坐標(biāo)是(5,8);③sin∠COA= ;④AC+OB=12
;④AC+OB=12 .其中正確的結(jié)論有
.其中正確的結(jié)論有 (x>0)的解析式,由反比例函數(shù)的解析式與直線BC的解析式聯(lián)立即可求出E點坐標(biāo);由sin∠COA=
(x>0)的解析式,由反比例函數(shù)的解析式與直線BC的解析式聯(lián)立即可求出E點坐標(biāo);由sin∠COA= 可求出∠COA的正弦值;根據(jù)A、C兩點的坐標(biāo)可求出AC的長,由OB•AC=160即可求出OB的長.
可求出∠COA的正弦值;根據(jù)A、C兩點的坐標(biāo)可求出AC的長,由OB•AC=160即可求出OB的長.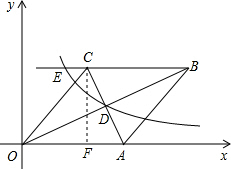 解:過點C作CF⊥x軸于點F,
解:過點C作CF⊥x軸于點F, OB•AC=
OB•AC= ×160=80,菱形OABC的邊長為10,
×160=80,菱形OABC的邊長為10, =
= =8,
=8, =
=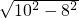 =6,
=6, ,
, ),即(8,4),
),即(8,4), (x>0)經(jīng)過D點,
(x>0)經(jīng)過D點, ,即k=32,
,即k=32,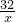 (x>0),故①錯誤;
(x>0),故①錯誤; ,解得x=4,y=8,
,解得x=4,y=8, =
= =
= ,故③正確;
,故③正確; =4
=4 ,
, =
= =8
=8 ,
, +8
+8 =12
=12 ,故④正確.
,故④正確.

科目:初中數(shù)學(xué) 來源: 題型:
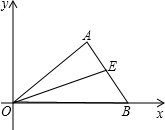 已知:如圖,在△AOB中,A(3,2),B(5,0),E(4,m),且點A、E、B在同一條直線上,求(1)m的值.(2)△AOE的面積.
已知:如圖,在△AOB中,A(3,2),B(5,0),E(4,m),且點A、E、B在同一條直線上,求(1)m的值.(2)△AOE的面積.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 21、已知:如圖,在△ABC中,分別延長中線BE、CD至N、M,使EN=EB,DM=DC,求證:點M、A、N三點在同一條直線上.
21、已知:如圖,在△ABC中,分別延長中線BE、CD至N、M,使EN=EB,DM=DC,求證:點M、A、N三點在同一條直線上.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
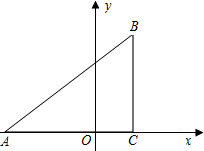 坐標(biāo)分別為A(-3,0),C(1,0),tan∠BAC=
坐標(biāo)分別為A(-3,0),C(1,0),tan∠BAC=| 3 | 4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 (2012•白下區(qū)一模)寫出下列命題的已知、求證,并完成證明過程.
(2012•白下區(qū)一模)寫出下列命題的已知、求證,并完成證明過程.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 (2013•浦東新區(qū)二模)已知:如圖,在△ABC中,點E在邊BC上,將△ABE沿直線AE折疊,點B恰好落在邊AC上的點D處,點F在線段AE的延長線上,如果∠FCA=∠B=2∠ACB,AB=5,AC=9.
(2013•浦東新區(qū)二模)已知:如圖,在△ABC中,點E在邊BC上,將△ABE沿直線AE折疊,點B恰好落在邊AC上的點D處,點F在線段AE的延長線上,如果∠FCA=∠B=2∠ACB,AB=5,AC=9.| BE | CF |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com