
【題目】如圖,已知二次函數 ![]() 的圖像經過點A(-1,-1)和點B(3,-9).
的圖像經過點A(-1,-1)和點B(3,-9).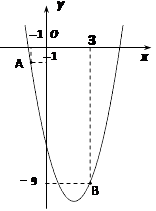
(1)求該二次函數的表達式;
(2)寫出該拋物線的對稱軸及頂點坐標;
(3)點P(m , m)與點Q均在該函數圖像上(其中m>0),且這兩點關于拋物線的對稱軸對稱,求m的值及點Q 到x軸的距離.
【答案】
(1)解:將A(﹣1,﹣1)和點B(3,﹣9)代入y=ax2﹣4x+c,
得 ![]() 解得
解得 ![]() ,
,
所以二次函數的表達式為y=x2﹣4x﹣6
(2)解:由y=x2﹣4x﹣6=(x﹣2)2﹣10可知:
對稱軸為x=2;頂點坐標為(2,﹣10)
(3)解:將P(m,m)坐標代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6.
解得m1=﹣1,m2=6.
因為m>0,所以m=﹣1不合題意,舍去.所以m=6,
所以P點坐標為(6,6);
因為點P與點Q關于對稱軸x=2對稱,所以點Q到x軸的距離為46.
【解析】(1)利用待定系數法將點A、點B的坐標代入函數解析式即可求出結果。
(2)利用配方法將函數解析式化成頂點式,即可求出結果。
(3)將點P的坐標代入函數解析式,得出關于m的一元二次方程,解方程求解,根據題意確定m的值,再根據二次函數的對稱性求出點Q的坐標。
【考點精析】根據題目的已知條件,利用二次函數的性質的相關知識可以得到問題的答案,需要掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:初中數學 來源: 題型:
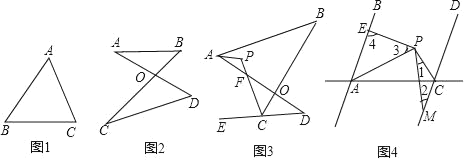
【題目】(1)如圖,請證明∠A+∠B+∠C=180°
(2)如圖的圖形我們把它稱為“8字形”,請證明∠A+∠B=∠C+∠D
(3)如圖,E在DC的延長線上,AP平分∠BAD,CP平分∠BCE,猜想∠P與∠B、∠D之間的關系,并證明
(4)如圖,AB∥CD,PA平分∠BAC,PC平分∠ACD,過點P作PM、PE交CD于M,交AB于E,則①∠1+∠2+∠3+∠4不變;②∠3+∠4﹣∠1﹣∠2不變,選擇正確的并給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E,點M在⊙O上,MD恰好經過圓心O,連接MB.
(1)若CD=16,BE=4,求⊙O的直徑;
(2)若∠M=∠D,求∠D的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果批發商銷售每箱進價為40元的蘋果,物價部門規定每箱售價不得高于55元,市場調查發現,若每箱以50元的價格調查,平均每天銷售90箱,價格每提高1元,平均每天少銷售3箱.
(1)求平均每天銷售量y(箱)與銷售價x(元/箱)之間的函數關系式.
(2)求該批發商平均每天的銷售利潤w(元)與銷售價x(元/箱)之間的函數關系式.
(3)當每箱蘋果的銷售價為多少元時,可以獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+3x+4與x軸交于A、B兩點,與y軸交于點C,點D在拋物線上且橫坐標為3.
(1)求A、B、C、D的坐標;
(2)求∠BCD的度數;
(3)求tan∠DBC的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某居民小區為了綠化小區環境,建設和諧家園,準備將一塊周長為76米的長方形空地,設計成長和寬分別相等的9塊小長方形,如圖所示,計劃在空地上種上各種花卉,經市場預測,綠化每平方米空地造價210元,請計算,要完成這塊綠化工程,預計花費多少元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,若![]() ,將點
,將點![]() 在
在![]() 內部,∠
內部,∠![]() ,∠
,∠![]() ,∠
,∠![]() 滿足的數量關系是 ,并說明理由.
滿足的數量關系是 ,并說明理由.
(2)在如圖1中,將直線![]() 繞點
繞點![]() 逆時針方向旋轉一定角度交直線
逆時針方向旋轉一定角度交直線![]() 于點
于點![]() ,如圖2,利用(1)中的結論(可以直接套用),求∠
,如圖2,利用(1)中的結論(可以直接套用),求∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() 之間有何數量關系?
之間有何數量關系?

(3)科技活動課上,雨軒同學制作了一個圖(3)的“飛旋鏢”,經測量發現∠![]() =
=![]() °,∠
°,∠![]() =
=![]() °,則∠
°,則∠![]() 與∠
與∠![]() 的數量關系是 .
的數量關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B在反比例函數 ![]() 的圖象上,且點A、B的橫坐標分別為a、2a(a>0),AC⊥x軸,垂足為C,且△AOC的面積為2,
的圖象上,且點A、B的橫坐標分別為a、2a(a>0),AC⊥x軸,垂足為C,且△AOC的面積為2,
(1)求該反比例函數的解析式;
(2)求△AOB的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com