
【題目】如圖,拋物線y=﹣x2+3x+4與x軸交于A、B兩點,與y軸交于點C,點D在拋物線上且橫坐標為3.
(1)求A、B、C、D的坐標;
(2)求∠BCD的度數;
(3)求tan∠DBC的值.
【答案】
(1)解:令y=0,則﹣x2+3x+4=0,
即(x+1)(x﹣4)=0.
解得:x1=﹣1,x2=4.
所以A(﹣1,0),B(4,0),
令x=0,得y=4,所以C(0,4),
當x=3時,y=﹣32+3×3+4=4,
所以D(3,4)。
(2)解:∵OC=OB=4,
∴∠ABC=45°,
∵C、D的縱坐標相同,
∴CD∥AB.
又∵OC=OB,
∴∠BCD=∠OBC=45°
(3)解:過點D作DE⊥BC于點E, 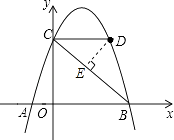
在Rt△OBC中,得BC=4 ![]() ,
,
在Rt△CDE中,∵CD=3,
∴CE=ED= ![]()
![]() ,
,
∴BE=BC﹣CE= ![]()
![]() ,
,
∴tan∠DBC= ![]() =
= ![]() .
.
【解析】(1)將y=0和x=0,x=3分別代入函數解析式,求出對應的自變量的值和對應的函數值,即可求出A、B、C、D的坐標。
(2)根據點B的橫坐標和點C的縱坐標相等,即可證出△OBC是等腰直角三角形,得出∠ABC=45°,再觀察點C、點D的縱坐標相等得出CD∥AB,根據平行線的性質即可求出結果。
(3)添加輔助線將∠DBC轉化到直角三角形中,因此過點D作DE⊥BC于點E,先根據點C和點D的坐標求出CD的長,在Rt△OBC中和在Rt△CDE中分別求出BC、DE的長,就可以求出BE的長,從而求得結果。
【考點精析】掌握拋物線與坐標軸的交點和勾股定理的概念是解答本題的根本,需要知道一元二次方程的解是其對應的二次函數的圖像與x軸的交點坐標.因此一元二次方程中的b2-4ac,在二次函數中表示圖像與x軸是否有交點.當b2-4ac>0時,圖像與x軸有兩個交點;當b2-4ac=0時,圖像與x軸有一個交點;當b2-4ac<0時,圖像與x軸沒有交點.;直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2.


科目:初中數學 來源: 題型:
【題目】某市開展一項自行車旅游活動,線路需經A,B,C,D四地,如圖,其中A,B,C三地在同一直線上,D地在A地北偏東30°方向,在C地北偏西45°方向,C地在A地北偏東75°方向.且BC=CD=20km,問沿上述線路從A地到D地的路程大約是多少?(最后結果保留整數,參考數據:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將兩個全等的直角三角形△ABD、△ACE拼在一起(圖(1)).令△ABD不動,
(1)若將△ACE繞點A逆時針旋轉,連接DE,M是DE的中點,連接MB、MC(圖(2)),證明:MB=MC.
(2)若將圖(1)中的CE向上平移,∠CAE不變,連接DE,M是DE的中點,連接MB、MC(圖(3)),判斷MB、MC的數量關系,并說明理由.
(3)在(2)中,若∠CAE的大小改變(圖(4)),其他條件不變,則(2)中的MB、MC的數量關系還成立嗎?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數 ![]() 的圖像經過點A(-1,-1)和點B(3,-9).
的圖像經過點A(-1,-1)和點B(3,-9).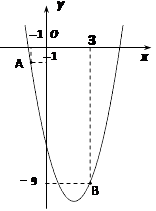
(1)求該二次函數的表達式;
(2)寫出該拋物線的對稱軸及頂點坐標;
(3)點P(m , m)與點Q均在該函數圖像上(其中m>0),且這兩點關于拋物線的對稱軸對稱,求m的值及點Q 到x軸的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:對于任何數a,符號[a]表示不大于a的最大整數.
例如:[5.7]=5,[5]=5,[﹣1.5]=﹣2.
(1)[﹣![]() ]= ;
]= ;
(2)如果[a]=3,那么a的取值范圍是 ;
(3)如果[![]() ]=﹣3,求滿足條件的所有整數x.
]=﹣3,求滿足條件的所有整數x.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著市民環保意識的增強,節慶期間煙花爆竹銷售量逐年下降.某市2012年銷售煙花爆竹20萬箱,到2014年煙花爆竹銷售量為9.8萬箱.求該市2012年到2014年煙花爆竹年銷售量的平均下降率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y= ![]() x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(一1,0).
x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(一1,0).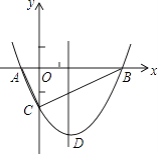
(1)求拋物線的解析式及頂點D的坐標;
(2)判斷△ABC的形狀,證明你的結論;
(3)點M是拋物線對稱軸上的一個動點,當△ACM周長最小時,求點M的坐標及△ACM的最小周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com