Question

已知:AB是⊙O中長為4的弦,P是⊙O上一動點,cos∠APB=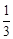, 問是否存在以A、P、B為頂點的面積最大的三角形?若不存在,試說明理由;若存在,求出這個三角形的面積.

 

Answer 1

【答案】

存在，4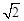

【解析】

試題分析：由題意可知AB不是直徑，故取優弧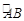的中點為P點,過P作PD⊥AB于D,

則PD是圓上所有的點中到AB 距離最大的點.當P為優弧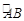的中點時,△APB的面積最大,連接PA、PB, 則等腰三角形APB即為所求,由作法知:圓心O必在PD上,連接AO,則由垂徑定理得AD=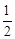AB=2.又∠AOD=∠1+∠2,可得∠AOD=∠2+∠1=∠2+∠3=∠APB,即可得到cos∠AOD的值，設OD=x,OA=3x,則即可表示出AD，再根據三角形的面積公式即可求得結果.

∵AB不是直徑(否則∠APB=90°,而由cos∠APB=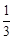 知∠APB<90°,矛盾)

∴取優弧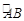的中點為P點,過P作PD⊥AB于D,

則PD是圓上所有的點中到AB 距離最大的點.

∵AB的長為定值,

∴當P為優弧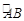的中點時,△APB的面積最大,連接PA、PB,

則等腰三角形APB即為所求.

由作法知:圓心O必在PD上,如圖所示,連接AO,則由垂徑定理得AD= 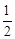 AB="2."

又∠AOD=∠1+∠2,而∠2=∠3,∠1=∠2

故∠AOD=∠2+∠1=∠2+∠3=∠APB,即cos∠AOD= ,

∴cos∠AOD=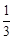,設OD=x,OA=3x,則AD= ,

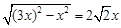即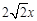="2" ,故x=,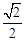

∴AO=3x=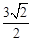,OD=x=,

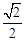∴PD=OP+OD=OA+OD=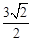+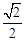=2,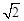

∴S△APB=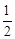AB·PD=4.

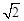考點：垂徑定理，等腰三角形的性質，勾股定理，直角三角形的性質

點評：本題綜合性強，知識點較多，因而這類問題在中考中比較常見，在各種題型中均有出現，一般難度較大，需多加關注.