如圖，AB∥CD，∠BAE=120°，∠DCE=30°，則∠AEC= 度．
90
【考點】平行線的性質．
【專題】綜合題．
【分析】延長AE交CD于點F，根據兩直線平行同旁內角互補可得∠BAE+∠EFC=180°，已知∠BAE的度數，不難求得∠EFC的度數，再根據三角形的外角的性質即可求得∠AEC的度數．
【解答】解：如圖，延長AE交CD于點F，
∵AB∥CD，
∴∠BAE+∠EFC=180°．
又∵∠BAE=120°，
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°，
又∵∠DCE=30°，
∴∠AEC=∠DCE+∠EFC=30°+60°=90°．
故答案為90．
【點評】此題主要考查學生對平行線的性質及三角形的外角性質的綜合運用，注意輔助線的添加方法．
閱讀快車系列答案科目：初中數學 來源： 題型：
如圖，直線AB，CD相交于點O，因為∠1+∠3=180°，∠2+∠3=180°，所以∠1=∠2．其推理依據是（ ）
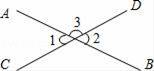
A．同角的余角相等 B．等角的余角相等
C．同角的補角相等 D．等角的補角相等
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，EF∥AD，∠1=∠2，∠BAC=65°．將下面求∠AGD的過程填寫完整．
解：∵EF∥AD（已知）
∴∠2= （ ）
又∵∠1=∠2（已知）
∴∠1= （等量代換）
∴AB∥ （ ）
∴∠BAC+ =180°（ ）
∵∠BAC=65°（已知）
∴∠AGD= ．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖所示第1個圖案是由黑白兩種顏色的正六邊形地面磚組成，第2個，第3個圖案可以看作是第1個圖案經過平移而得，那么第5個圖案中有白色地面磚____塊，第
個圖案中有白色地面磚的塊數為______。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
B．
D．
）﹣1． 
﹣
，4，
，2π，0.15，
中，有理數的個數為B，無理數的個數為A，則A﹣B的值為（ ）
