
【題目】綜合探究
問題情境:
我們在第十一章《三角形》中學習了三角形的邊與角的性質,在第十二章《全等三角形》中學習了全等三角形的性質和判定.在一些探究題中經常用以上知識轉化角和邊,進而解決問題.
問題初探:
如圖1,在△ABC中,∠ACB=90°,AC=BC,點D為直線AB上的一個動點(D與A,B不重合),連接CD,以CD為直角邊作等腰直角三角形CDE,連接BE.


(1)當點D在線段AB上時,AD與BE的數量關系是 ;位置關系是 ;AB,BD,BE三條線段之間的關系是 .
類比再探:
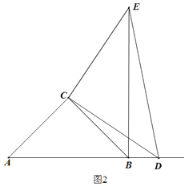
(2)如圖2,當點D運動到AB的延長線上時,AD與BE還存在(1)中的位置關系嗎?若存在,請說明理由.同時探索AB,BD,BE三條線段之間的數量關系,并說明理由.
能力提升:
(3)如圖3,當點D運動到BA的延長線上時,若AB=7,AD=2,則AE= .
【答案】(1)相等,垂直,AB=BD+BE;(2)成立,AB= BE-BD;(3)9.
【解析】
(1)根據等腰直角三角形的性質得到AC=BC,∠ACD=∠BCE,DC=EC,即可證明△ADC≌△BEC,根據全等三角形的性質即可得出結論;
(2)同理可得結論;
(3)同理可證:△AEC≌△BDC,根據全等三角形的性質可得AE=BD=AB+AD,即可得到結論.
(1)∵△ABC是等腰直角三角形,∴AC=BC,∠A=∠ABC=45°,∠ACB=90°.
∵△DCE是等腰直角三角形,∴CD=CE,∠DCE=90°,∴∠ACD=∠BCE.
在△ADC和△BEC中,∵AC=BC,∠ACD=∠BCE,DC=EC,∴△ADC≌△BEC,∴AD=BE,∠A=∠CBE=45°,∴∠ABE=∠ABC+∠CBE=45°+45°=90°,∴AB⊥BE.
∵AD=BE,∴AB=AD+BD=BD+BE.
故答案為:相等,垂直,AB=BD+BE.
(2)成立,AB= BE-BD.理由如下:
∵△ABC是等腰直角三角形,∴AC=BC,∠A=∠ABC=45°,∠ACB=90°.
∵△DCE是等腰直角三角形,∴CD=CE,∠DCE=90°,∴∠ACD=∠BCE.
在△ADC和△BEC中,∵AC=BC,∠ACD=∠BCE,DC=EC,∴△ADC≌△BEC,∴AD=BE,∠A=∠CBE=45°,∴∠ABE=∠ABC+∠CBE=45°+45°=90°,∴AB⊥BE.
∵AD=BE,∴AB=AD-BD= BE-BD.
故答案為:垂直,AB= BE-BD.
(3)同理可證:△AEC≌△BDC,∴AE=BD,∴AE=AB+AD=7+2=9.
故答案為:9.


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:
【題目】某烤鴨店在確定烤鴨的烤制時間時,主要依據的是如表數據:
鴨的質量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
烤制時間/分鐘 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
設鴨的質量為x千克,烤制時間為t,估計當x=2.2千克時,t的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】早晨,小明步行到離家900米的學校去上學,到學校時發現眼鏡忘在家中,于是他立即按原路步行回家,拿到眼鏡后立即按原路騎自行車返回學校.已知小明步行從學校到家所用的時間比他騎自行車從家到學校所用的時間多10分鐘,小明騎自行車速度是步行速度的3倍.
(1)求小明步行速度(單位:米/分)是多少;
(2)下午放學后,小明騎自行車回到家,然后步行去圖書館,如果小明騎自行車和步行的速度不變,小明步行從家到圖書館的時間不超過騎自行車從學校到家時間的2倍,那么小明家與圖書館之間的路程最多是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
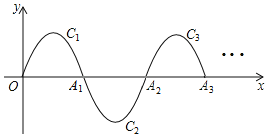
【題目】如圖,一段拋物線:![]() ,記為
,記為![]() ,它與x軸交于點O,
,它與x軸交于點O,![]() ;將
;將![]() 繞點
繞點![]() 旋轉
旋轉![]() 得
得![]() ,交x軸于點
,交x軸于點![]() ;將
;將![]() 繞點
繞點![]() 旋轉
旋轉![]() 得
得![]() ,交x軸于點
,交x軸于點![]() ;
;![]() 如此進行下去,得到一“波浪線”,若點
如此進行下去,得到一“波浪線”,若點![]() 在此“波浪線”上,則m的值為
在此“波浪線”上,則m的值為![]()
![]()
A. 4 B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為保護和改善環境,發展新經濟,國家出臺了不限行、不限購等諸多新能源汽車優惠政策鼓勵新能源汽車的發展,為響應號召,某市某汽車專賣店銷售A,B兩種型號的新能源汽車共25輛,這兩種型號的新能源汽車的進價、售價如下表:
進價 | 售價 | |
A型 | 10 |
|
B型 | 15 |
|
![]() 如何進貨,進貨款恰好為325萬元?
如何進貨,進貨款恰好為325萬元?
![]() 如何進貨,該專賣店售完A,B兩種型號的新能源汽車后獲利最多且不超過進貨價的
如何進貨,該專賣店售完A,B兩種型號的新能源汽車后獲利最多且不超過進貨價的![]() ,此時利潤為多少元?
,此時利潤為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市市民“綠色出行”方式的情況,某校數學興趣小組以問卷調查的形式,隨機調查了某市部分出行市民的主要出行方式(參與問卷調查的市民都只從以下五個種類中選擇一類),并將調查結果繪制成如下不完整的統計圖.
種類 | A | B | C | D | E |
出行方式 | 共享單車 | 步行 | 公交車 | 的士 | 私家車 |

根據以上信息,回答下列問題:
(1)參與本次問卷調查的市民共有 人,其中選擇B類的人數有 人;
(2)在扇形統計圖中,求A類對應扇形圓心角α的度數,并補全條形統計圖;
(3)該市約有12萬人出行,若將A,B,C這三類出行方式均視為“綠色出行”方式,請估計該市“綠色出行”方式的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對一個矩形ABCD及![]() 給出如下定義:在同一平面內,如果
給出如下定義:在同一平面內,如果![]() 上存在一點,使得這點到矩形ABCD的四個頂點的距離相等,那么稱矩形ABCD是
上存在一點,使得這點到矩形ABCD的四個頂點的距離相等,那么稱矩形ABCD是![]() 的“隨從矩形”
的“隨從矩形”![]() 如圖,在平面直角坐標系xOy中,直線l:
如圖,在平面直角坐標系xOy中,直線l:![]() 交x軸于點M,
交x軸于點M,![]() 的半徑為4,矩形ABCD沿直線運動
的半徑為4,矩形ABCD沿直線運動![]() 在直線l上
在直線l上![]() ,
,![]() ,
,![]() 軸,當矩形ABCD是
軸,當矩形ABCD是![]() 的“隨從矩形”時,點A的坐標為______.
的“隨從矩形”時,點A的坐標為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com