Question

在Rt△ABC中，∠ACB=90°，CD⊥AB于D，若AB=10，AC-BC=2，求CD的長．

Answer 1

【答案】分析：此題先設BC=x，利用勾股定理，可求出BC和AC，再利用三角形面積不變，用兩種方法表示，即可求出CD的長．
解答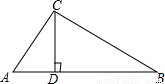：解：設BC=a，AC=b，AB=c，則有b-a=2
由a²+b²=c²得（b-a）²+2ab=c²，即
4+2ab=10²，
∴ab=48
∴ab=×10•CD=24，
∴CD=4.8．
點評：本題利用了勾股定理以及直角三角形的面積公式（其面積=×兩直角邊的積=×斜邊×斜邊上的高）．