
【題目】如圖,△ABC的周長為1,E、F、G分別為AB、AC、BC的中點,A′、B′、C′分別為EF、EG、GF的中點,如果△ABC、△EFG、△A′B′C′分別為第1個、第2個、第3個三角形,按照上述方法繼續作三角形,那么第n個三角形的周長是__________________.

【答案】![]()
【解析】
根據E、F、G分別為AB、AC、BC的中點,可以判斷EF、FG、EG為三角形中位線,利用中位線定理求出EF、FG、EG與BC、AB、CA的長度關系即可求得△EFG的周長是△ABC周長的一半,△A'B'C'的周長是△EFG的周長的一半,以此類推,可以求得第n個三角形的周長.
∵如圖,△ABC的周長為1,E、F、G分別為AB、AC、BC的中點,∴EF、FG、EG為三角形中位線,∴EF![]() BC,EG
BC,EG![]() AC,FG
AC,FG![]() AB,∴EF+FG+EG
AB,∴EF+FG+EG![]() (BC+AC+AB)
(BC+AC+AB)![]() ,即△EFG的周長是△ABC周長的一半.
,即△EFG的周長是△ABC周長的一半.
同理,△A'B'C'的周長是△EFG的周長的一半,即△A'B'C'的周長為![]() 1
1![]() =
=![]() .
.
以此類推,第n個小三角形的周長是第一個三角形周長的1×(![]() )n﹣1=
)n﹣1=![]() .
.
故答案為:![]() .
.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案科目:初中數學 來源: 題型:
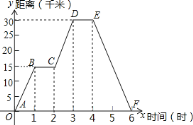
【題目】小明同學騎自行車去濱海港郊游,中途休息了一段時間。如圖表示他離家的距離y(千米)與所用的時間s(小時)之間關系的函數圖像
(1)根據圖像回答:小明家離濱海港 千米,小明到達濱海港時用了 小時;
(2)直線CD的函數解析式為 ;
(3)小明出發幾小時,離家12千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個有50個奇數排成的數陣,用如圖所示的框去框住四個數,并求出這四個數的和,在下列給出的備選答案中,有可能是這四個數的和的是( )

A. 114 B. 122 C. 220 D. 84
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知![]() 頂點的坐標分別為
頂點的坐標分別為![]() ,且
,且![]() 是由
是由![]() 旋轉得到.若點
旋轉得到.若點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 軸上,要使四邊形
軸上,要使四邊形![]() 為平行四邊形,則滿足條件的點
為平行四邊形,則滿足條件的點![]() 的坐標為______.
的坐標為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九(1)班數學興趣小組經過市場調查,整理出某種商品在第x(1≤x≤90)天的售價與銷量的相關信息如下表:
時間x(天) | 1≤x<50 | 50≤x≤90 |
售價(元/件) | x+40 | 90 |
每天銷量(件) | 200-2x | |
已知該商品的進價為每件30元,設銷售該商品每天的利潤為y元。
(1)求出y與x的函數關系式;
(2)問銷售該商品第幾天時,當天的銷售利潤最大?最大利潤是多少?
(3)該商品在銷售過程中,共有多少天每天的銷售利潤不低于4800元?請直接寫出結果。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB為⊙O的直徑,點E在⊙O上,∠EAB的平分線交⊙O于點C,過點C作AE的垂線,垂足為D,直線DC與AB的延長線交于點P.

(1)判斷直線PC與⊙O的位置關系,并說明理由;
(2)若tan∠P=![]() ,AD=6,求線段AE的長.
,AD=6,求線段AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知P是⊙O外一點,PO交⊙O于點C,OC=CP=2,弦AB⊥OC,∠AOC的度數為60°,連接PB.

(1)求BC的長;
(2)求證:PB是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,對角線AC、BD相交于點O,下列條件不能判定這個四邊形是平行四邊形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com