
【題目】已知:C是線段AB所在平面內任意一點,分別以AC、BC為邊,在AB同側作等邊三角形ACE和BCD,聯結AD、BE交于點P.
(1)如圖1,當點C在線段AB上移動時,線段AD與BE的數量關系是: .
(2)如圖2,當點C在直線AB外,且∠ACB<120°,上面的結論是否還成立?若成立請證明,不成立說明理由.
(3)在(2)的條件下,∠APE大小是否隨著∠ACB的大小發生變化而發生變化,若變化寫出變化規律,若不變,請求出∠APE的度數.
【答案】
(1)解:∵△ACE和△BCD都是等邊三角形,
∴∠ACE=∠DCB=60°,CA=CE,CD=CB,
∴∠ACE+∠DCE=∠DCB+∠DCE,即∠ACD=∠ECB,
在△ECB和△ACD中,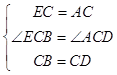 ,
,
∴△ECB≌△ACD,
∴AD=BE,
故答案為:AD=BE
(2)
解:AD=BE成立.
證明:∵△ACE和△BCD是等邊三角形,
∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD,
在△ECB和△ACD中,
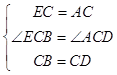 ,
,
∴△ECB≌△ACD(SAS),
∴BE=AD;
(3)
解:∠APE不隨著∠ACB的大小發生變化,始終是60°,
如圖2
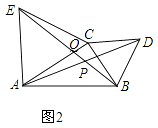
設BE與AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC,
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°,
∴∠APQ=∠ECQ=60°,即∠APE=60°.
【解析】(1)根據等邊三角形的性質得到∠ACE=∠DCB=60°,CA=CE,CD=CB,根據全等三角形的判定定理得到△ECB≌△ACD,根據全等三角形的性質證明;(2)根據等邊三角形的性質得到∠ACE=∠DCB=60°,CA=CE,CD=CB,根據全等三角形的判定定理得到△ECB≌△ACD,根據全等三角形的性質證明;(3)根據全等三角形的性質得到∠BEC=∠DAC,根據三角形內角和定理計算即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數![]() (k>0).
(k>0).
(1)當k=![]() 時,求這個二次函數的頂點坐標;
時,求這個二次函數的頂點坐標;
(2)求證:關于x的一元次方程![]() 有兩個不相等的實數根;
有兩個不相等的實數根;
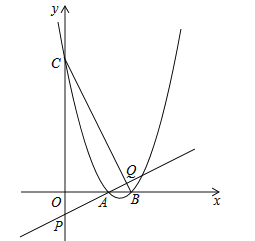
(3)如圖,該二次函數與x軸交于A、B兩點(A點在B點的左側),與y軸交于C點,P是y軸負半軸上一點,且OP=1,直線AP交BC于點Q,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有16筐白菜,以每筐30千克為標準,超過或不足的分別用正、負來表示,記錄如下:
(1)16筐白菜中,最重的一筐比最輕的一筐要重多少千克?
(2)與標準質量比較,16筐白菜總計超過或不足多少千克?
(3)若白菜每千克售價3元,則出售這16筐白菜可賣多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了迎接春節,某縣準備用燈籠美化濱河路,許采用A、B兩種不同造型的燈籠共600個.且A型燈籠的數量比B型燈籠的 ![]() 多15個.
多15個.
(1)求A、B兩種燈籠各需多少個?
(2)已知A、B型燈籠的單價分別為40元、30元,則這次美化工程需多少費用?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中: 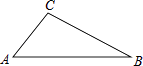
(1)用直尺和圓規,在AB上找一點D,使點D到B、C兩點的距離相等(不寫作法.保留作圖痕跡)
(2)連接CD,已知CD=AC,∠B=25°,求∠ACB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大于1的正整數m的三次冪可“分裂”成若干個連續奇數的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3分裂后,其中有一個奇數是123,則m的值是( )
A.9
B.10
C.11
D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明一家三口國慶節隨旅游團去九寨溝旅游,共花費人民幣5600元,他把旅途費用支出情況制成了如下的統計圖.請你根據統計圖解決下列問題:
(1)哪一部分支出的費用占整個支出的 ![]() ?
?
(2)小明一家在食宿上用去多少元?
(3)小明一家支出的路費共多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠MON=36°,OE平分∠MON,點A,B分別是射線OM,OE,上的動點(A,B不與點O重合),點D是線段OB上的動點,連接AD并延長交射線ON于點C,設∠OAC=x,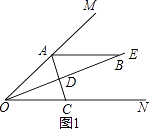
(1)如圖1,若AB∥ON,則
①∠ABO的度數是;
②當∠BAD=∠ABD時,x=;
當∠BAD=∠BDA時,x=;
(2)如圖2,若AB⊥OM,則是否存在這樣的x的值,使得△ABD中有兩個相等的角?若存在,求出x的值;若不存在,請說明理由.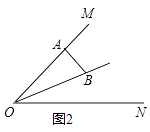
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com