
【題目】綜合與探究
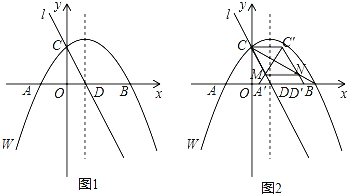
如圖1,在平面直角坐標系xOy中,拋物線W的函數表達式為y=﹣![]() x2+
x2+![]() x+4.拋物線W與x軸交于A,B兩點(點B在點A的右側,與y軸交于點C,它的對稱軸與x軸交于點D,直線l經過C、D兩點.
x+4.拋物線W與x軸交于A,B兩點(點B在點A的右側,與y軸交于點C,它的對稱軸與x軸交于點D,直線l經過C、D兩點.
(1)求A、B兩點的坐標及直線l的函數表達式.
(2)將拋物線W沿x軸向右平移得到拋物線W′,設拋物線W′的對稱軸與直線l交于點F,當△ACF為直角三角形時,求點F的坐標,并直接寫出此時拋物線W′的函數表達式.
(3)如圖2,連接AC,CB,將△ACD沿x軸向右平移m個單位(0<m≤5),得到△A′C′D′.設A′C交直線l于點M,C′D′交CB于點N,連接CC′,MN.求四邊形CMNC′的面積(用含m的代數式表示).
【答案】(1)點A坐標為(﹣3,0),點B的坐標為(7,0),y=﹣2x+4;(2) 點F的坐標為(5,﹣6),y=﹣![]() x2+
x2+![]() x;(3) 四邊形CMNC′的面積為
x;(3) 四邊形CMNC′的面積為![]() m2.
m2.
【解析】
根據拋物線的解析式,令y=0即可求出兩點的坐標.根據拋物線的解析式可分別求出C,D兩點的坐標,再用待定系數法即可求出直線的表達式.
根據題意,利用角的等量關系可以得到∠1=∠3,進而得到tan∠1=tan∠3,根據三角函數的計算方法列出等式,根據一次函數的解析式設點![]() 的坐標為(xF,﹣2xF+4),將各線段的長度代入等式即可求出點F的坐標,再根據平移的法則即可求出w′的表達式.
的坐標為(xF,﹣2xF+4),將各線段的長度代入等式即可求出點F的坐標,再根據平移的法則即可求出w′的表達式.
根據平移,可以得到點C′,A′,D′的坐標,再根據待定系數法可以得到直線A′C′,BC,C′D′的解析式,根據交點的計算方法列方程組可以求得點M,N的坐標,根據平移的定義和平行四邊形的定義可知四邊形CMNC′是平行四邊形,再根據平行四邊形面積的計算方法可以得到平行四邊形CMNC′的面積.
(1)當y=0時,﹣![]() x2+
x2+![]() +4=0,解得x1=﹣3,x2=7,
+4=0,解得x1=﹣3,x2=7,
∴點A坐標為(﹣3,0),點B的坐標為(7,0).
∵﹣![]() =
=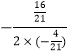
∴拋物線w的對稱軸為直線x=2,
∴點D坐標為(2,0).
當x=0時,y=4,
∴點C的坐標為(0,4).
設直線l的表達式為y=kx+b,
![]()
解得![]()
∴直線l的解析式為y=﹣2x+4;
(2)∵拋物線w向右平移,只有一種情況符合要求,
即∠FAC=90°,如圖.
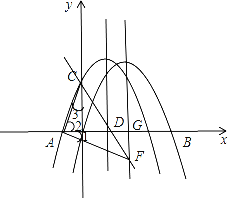
此時拋物線w′的對稱軸與x軸的交點為G,
∵∠1+∠2=90°∠2+∠3=90°,
∴∠1=∠3,
∴tan∠1=tan∠3,
∴![]() =
=![]() .設點F的坐標為(xF,﹣2xF+4),
.設點F的坐標為(xF,﹣2xF+4),
∴![]() =
=![]() ,解得xF=5,﹣2xF+4=﹣6,
,解得xF=5,﹣2xF+4=﹣6,
∴點F的坐標為(5,﹣6),此時拋物線w′的函數表達式為y=﹣![]() x2+
x2+![]() x;
x;
(3)由平移可得:點C′,點A′,點D′的坐標分別為C′(m,4),A′(﹣3+m,0),D′(2+m,0),CC′∥x軸,C′D′∥CD,
可用待定系數法求得
直線A′C′的表達式為y=![]() x+4﹣
x+4﹣![]() m,
m,
直線BC的表達式為y=﹣![]() x+4,
x+4,
直線C′D′的表達式為y=﹣2x+2m+4,
分別解方程組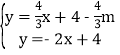 和
和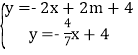
解得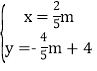 和
和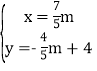
∴點M的坐標為(![]() m,﹣
m,﹣![]() m+4),點N的坐標為(
m+4),點N的坐標為(![]() m,﹣
m,﹣![]() m+4),
m+4),
∴yM=yN
∴MN∥x軸,
∵CC′∥x軸,
∴CC′∥MN.
∵C′D′∥CD,
∴四邊形CMNC′是平行四邊形,
∴S=m[4﹣(﹣![]() m+4)]
m+4)]
=![]() m2
m2


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:初中數學 來源: 題型:
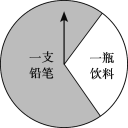
【題目】某商場有一個可以自由轉動的圓形轉盤(如圖).規定:顧客購物100元以上可以獲得一次轉動轉盤的機會,當轉盤停止時,指針落在哪一個區域就獲得相應的獎品(指針指向兩個扇形的交線時,當作指向右邊的扇形).下表是活動進行中的一組統計數據:
轉動轉盤的次數n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“鉛筆”的次數m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“鉛筆”的頻率 (結果保留小數點后兩位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)轉動該轉盤一次,獲得鉛筆的概率約為_______;(結果保留小數點后一位)
(2)鉛筆每只0.5元,飲料每瓶3元,經統計該商場每天約有4000名顧客參加抽獎活動,請計算該商場每天需要支出的獎品費用;
(3)在(2)的條件下,該商場想把每天支出的獎品費用控制在3000元左右,則轉盤上“一瓶飲料”區域的圓心角應調整為______度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在二次函數y=-x2+bx+c中,函數y與自變量x的部分對應值如下表:
x | …… | -2 | 0 | 3 | 4 | …… |
y | …… | -7 | m | n | -7 | …… |
則m、n的大小關系為( )
A. m>n B. m<n C. m=n D. 無法確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,對正方形ABCD及其內部的每個點進行如下操作:把每個點的橫、縱坐標都乘以同一個實數a,將得到的點先向右平移m個單位,再向上平移n個單位(m>0,n>0),得到正方形A'B'C'D'及其內部的點,其中點A、B的對應點分別為A',B'.已知正方形ABCD內部的一個點F經過上述操作后得到的對應點F'與點F重合,則點F的坐標是( )
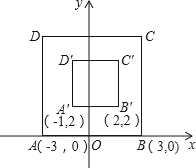
A. (1,4) B. (1,5) C. (﹣1,4) D. (4,1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB是⊙O的直徑,弦CD⊥AB于H,過CD延長線上一點E作⊙O的切線交AB的延長線于F,切點為G,連接AG交CD于K.
(1)如圖1,求證:KE=GE;
(2)如圖2,連接CABG,若∠FGB=![]() ∠ACH,求證:CA∥FE;
∠ACH,求證:CA∥FE;
(3)如圖3,在(2)的條件下,連接CG交AB于點N,若sinE=![]() ,AK=
,AK=![]() ,求CN的長.
,求CN的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠A=∠B=90°,P是線段AB上的一個動點.
(1)若AD=2,BC=6,AB=8,且以A,D,P為頂點的三角形與以B,C,P為頂點的三角形相似,求AP的長;
(2)若AD=a,BC=b,AB=m,則當a,b,m滿足什么關系時,一定存在點P使△ADP∽△BPC?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】反比例函數y=![]() (k為常數,且k≠0)的圖象經過點A(1,3)、B(3,m).
(k為常數,且k≠0)的圖象經過點A(1,3)、B(3,m).
(1)求反比例函數的解析式及B點的坐標;
(2)在x軸上找一點P,使PA+PB的值最小,求滿足條件的點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一艘在南北航線上的測量船,于A點處測得海島B在點A的南偏東30°方向,繼續向南航行30海里到達C點時,測得海島B在C點的北偏東15°方向,那么海島B離此航線的最近距離是(結果保留小數點后兩位)(參考數據:![]() )( )
)( )
A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里
查看答案和解析>>
科目:初中數學 來源: 題型:
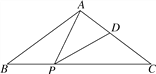
【題目】如圖,在△ABC中,AB=AC,點P、D分別是BC、AC邊上的點,且∠APD=∠B.
(1)求證:AC·CD=CP·BP;
(2)若AB=10,BC=12,當PD∥AB時,求BP的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com