
【題目】如圖,已知△ABC為直角三角形,∠C=90°,邊BC是⊙0的切線,切點為D,AB經過圓心O并與圓相交于點E,連接AD.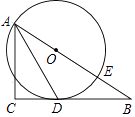
(1)求證:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半徑.
,求⊙O的半徑.
【答案】
(1)證明:連接OD,
∵BC是⊙O的切線,
∴OD⊥BC,
∠ODB=∠C=90°
∴OD∥AC,
∴∠ODA=∠CAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠CAD,即AD平分∠BAC
(2)解:連接DE, 
∵AE是⊙O的直徑,
∴∠ADE=90°,
∵∠OAD=∠CAD,tan∠DAC= ![]() ,
,
∴tan∠EAD= ![]() ,
,
∵tan∠DAC= ![]() ,AC=8,
,AC=8,
∴CD=6,
由勾股定理得,AD= ![]() =10,
=10,
∴ ![]() =
= ![]() ,
,
解得,DE= ![]() ,
,
∴AE= ![]() =
= ![]() ,
,
∴⊙O的半徑為 ![]() .
.
【解析】(1)已知圓的切線,常添加的輔助線是“連半徑,得垂直”。已知BC是⊙0的切線,所以連半徑OD,得到OD⊥BC,再由平行線的性質和等腰三角形的性質就可證得結論;(2)要求此圓的半徑,轉化為求直徑AE的長,已知圓的直徑,常添加的輔助線是“連接一條弦,得直徑所對的圓周角是直角”,方法一:連接DE,得到Rt△ADE,再根據正切的定義和勾股定理可得到圓的半徑,方法二求出AD的長后,也可以證明△ACD![]() △ADE求得AE的長,即可得到此圓的半徑長。
△ADE求得AE的長,即可得到此圓的半徑長。
【考點精析】認真審題,首先需要了解平行線的判定與性質(由角的相等或互補(數量關系)的條件,得到兩條直線平行(位置關系)這是平行線的判定;由平行線(位置關系)得到有關角相等或互補(數量關系)的結論是平行線的性質),還要掌握等腰三角形的性質(等腰三角形的兩個底角相等(簡稱:等邊對等角))的相關知識才是答題的關鍵.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:
【題目】如圖,點M是AB的中點,點P在MB上.分別以AP,PB為邊,作正方形APCD和正方形PBEF,連結MD和ME.設AP=a,BP=b,且a+b=10,ab=20.則圖中陰影部分的面積為________.
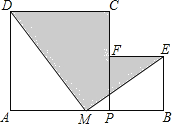
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD.∠1=∠2,∠3=∠4,試說明 AD∥BE,請你將下面解答過程填寫完整.

解:∵AB∥CD,
∴∠4= ( )
∵∠3=∠4
∴∠3= (等量代換)
∵∠1=∠2
∴∠1+∠CAF=∠2+∠CAE 即∠BAE= .
∴∠3= ( )
∴AD∥BE( ).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知 AD⊥BC,垂足為點 D,EF⊥BC,垂足為點 F,∠1+∠2=180°, 請填寫∠CGD=∠CAB 的理由.

解:因為 AD⊥BC,EF⊥BC( )
所以∠ADC=90°,∠EFD=90°( )
得∠ADC=∠EFD( )
所以 AD//EF( )
得∠2+∠3=180° ( )
又因為∠1+∠2=180°(已知)
所以∠1=∠3( )
所以 DG//AB( )
所以∠CGD=∠CAB( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周長為36 cm,點P從點A開始沿AB邊向B點以每秒1cm的速度移動;點Q從點B沿BC邊向點C以每秒2cm的速度移動,如果同時出發,則過3s時,△BPQ的面積為____cm2.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在四邊形ABCD中,∠DAB被對角線AC平分,且AC2=ABAD,我們稱該四邊形為“可分四邊形”,∠DAB稱為“可分角”.
(1)如圖2,若四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,且∠DCB=∠DAB,則∠DAB=°.
(2)如圖3,在四邊形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求證:四邊形ABCD為“可分四邊形”;
(3)現有四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,且AC=4,BC=2,∠D=90°,求AD的長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,真命題是( )
A. 如果三角形三個角的度數比是3:4:5,那么這個三角形是直角三角形
B. 如果直角三角形兩直角邊的長分別為a和b,那么斜邊的長為a2+b2
C. 若三角形三邊長的比為1:2:3,則這個三角形是直角三角形
D. 如果直角三角形兩直角邊分別為a和b,斜邊為c,那么斜邊上的高h的長為![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將長方形紙片ABCD折疊,使點D與點B重合,點C落在點C'處,折痕為EF,若∠ABE=25°,則∠EFC'的度數為( )
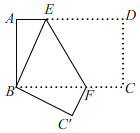
A.122.5°B.130°C.135°D.140°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,BC=16cm,AC=12cm,點P從點B出發,沿BC以2cm/s的速度向點C移動,點Q從點C出發,以1cm/s的速度向點A移動,若點P、Q分別從點B、C同時出發,設運動時間為t s,當t=時,△CPQ與△CBA相似.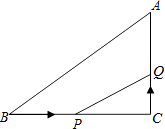
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com