
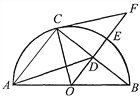
【題目】如圖,AB是半圓O的直徑,E是弧BC的中點,OE交弦BC于點D,點F為OE的延長線上一點且OC2=OD·OF.
(1)求證:CF為⊙O的切線.
(2)已知DE=2, ![]() .
.
①求⊙O的半徑;②求sin∠BAD的值

【答案】(1)證明見解析(2)①5②![]()
【解析】試題分析:(1)連接OC,利用同圓的半徑相等和直徑所對的圓周角為直角,得∠OCF=90°,CF是 O的切線;(2)①設 O的半徑為r,根據勾股定理列方程解出即可;②過點D作DG⊥OB,利用勾股定理分別求出DG,AG,即可求出sin∠BAD的值.
試題解析:
(1)![]() ,∠COD是公共角
,∠COD是公共角
∴△COD∽△COF,
∴∠F=∠OCD,
又E是弧BC的中點,
∴∠COE=∠BOE,
∵OC=OB,
∴OD⊥BC
∴OD⊥BC,
∴CF為⊙O的切線.
(2)①![]() ,設BC=4x,
,設BC=4x,
則AC=3x,AB=5x,OE=2.5x,
OD=1.5x,DE=x=2,2.5x=2.5;
∴⊙O的半徑為5;
②作DG⊥OB于G,Rt△BOD中,DG=OD×BD÷OB,
∴DG=3×4÷5=![]() ,
,
Rt△ACD中,AC=6,AB=4,
∴AD=![]() ;
;
Rt△AGD中,sin∠BAD=DG÷AD=![]()


科目:初中數學 來源: 題型:
【題目】2014年吉林省對全省供熱管網進行改造,改造后全年二氧化碳排放量共減少7620000噸,7620000這個數用科學記數法表示為( )
A.762×104
B.76.2×105
C.7.62×106
D.0.762×107
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,已知E為BC的中點,連接AE并延長交DC的延長線于點F,連接BF. 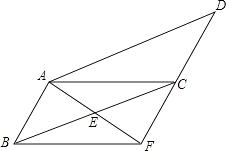
(1)求證:AB=CF;
(2)當BC與AF滿足什么數量關系時,四邊形ABFC是矩形,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com