【題目】如圖，在每個小正方形的邊長為
的網格中，
的頂點
均落在格點上，
（1）
的長等于________；
（2）在△ABC的內部有一點P，滿足S△PAB：S△PBC：S△PCA=1：2：3，請在如圖所示的網格中，用無刻度的直尺，畫出點P，并簡要說明點P的位置是如何找到的（不要求證明）．
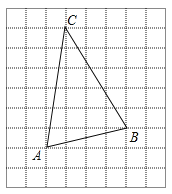
【答案】（1）
；（2）答案見解析
【解析】
（1）利用勾股定理即可解決問題；
（2）如圖AC與網格相交，得到點D、E，取格點F，連接FB并且延長，與網格相交，得到M，N，G．連接DN，EM，DG，DN與EM相交于點P，點P即為所求．
解：(1)
故答案為：；
（2）如圖AC與網格相交，得到點D、E，取格點F，連接FB并且延長，與網格相交，得到M，N，G．連接DN，EM，DG，DN與EM相交于點P，點P即為所求．
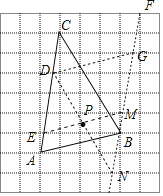
理由：平行四邊形ABME的面積：平行四邊形CDNB的面積：平行四邊形DEMG的面積=1：2：3，
△PAB的面積=
平行四邊形ABME的面積，△PBC的面積=平行四邊形CDNB的面積，△PAC的面積=△PNG的面積=△DGN的面積=平行四邊形DEMG的面積，
∴S△PAB：S△PBC：S△PCA=1：2：3．
科目：初中數學 來源： 題型：
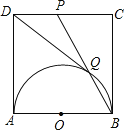
【題目】如圖，正方形ABCD的邊長為1，以AB為直徑作半圓，點P是CD中點，BP與半圓交于點Q，連結DQ，給出如下結論：①
；②
；③
；④
，其中正確結論是______
填寫序號
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小麗同學學習了統計知識后，帶領班級“課外活動小組”，隨機調查了某轄區若干名居民的年齡，并將調查數據繪制成圖①和圖②兩幅尚不完整的統計圖．
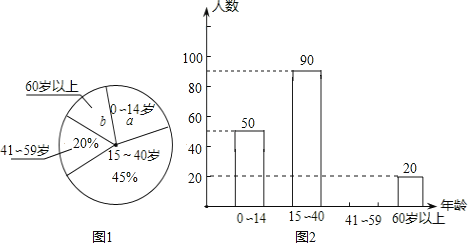
請你根據圖中的信息，解答下列各題：
（1）共抽查了_____名居民的年齡，扇形統計圖中
_____，
______；
（2）補全條形統計圖；
（3）若該轄區居民約有2600人，請你估計年齡在15～59歲的居民人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校初級中學數學興趣小組為了解本校學生年齡情況，隨機調查了本校部分學生的年齡，根據所調查的學生的年齡(單位：歲)，繪制出如下的統計圖①和圖②，請根據相關信息，解答下列問題：
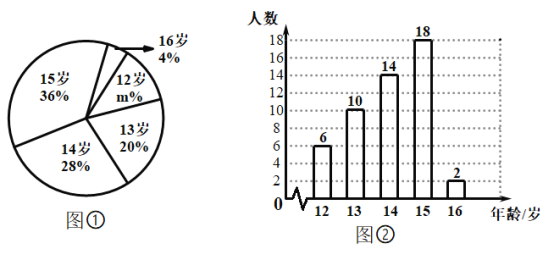
（1）本次接受調查的學生人數為_______，圖①中 
的值為 ；
（2）求統計的這組學生年齡數據的平均數、眾數和中位數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
的正方形網格中，每個小正方形的邊長均為1，
的三個頂點均在小正方形的頂點上．
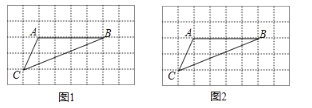
（1）在圖1中畫一個
（點
在小正方形的頂點上），使的周長等于的周長，且以
、
、
、為頂點的四邊形是軸對稱圖形；
（2）在圖2中畫
（點
在小正方形的頂點上），使的周長等于的周長，且以、、、為頂點的四邊形是中心對稱圖形；
（3）直接寫出圖2中四邊形的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖①是由五個完全相同的小正方體組成的立體圖形．將圖①中的一個小正方體改變位置后如圖②，則三視圖發生改變的是（ ）
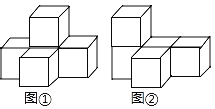
A.主視圖B.俯視圖
C.左視圖D.主視圖、俯視圖和左視圖都改變
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數y＝﹣x2+bx+c的圖象經過點A（3，1），點B（0，4）．
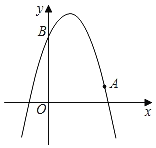
（1）求該二次函數的表達式及頂點坐標；
（2）點C（m，n）在該二次函數圖象上．
①當m＝﹣1時，求n的值；
②當m≤x≤3時，n最大值為5，最小值為1，請根據圖象直接寫出m的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
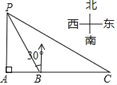
【題目】如圖，某海監船以20海里/小時的速度在某海域執行巡航任務，當海監船由西向東航行至A處時，測得島嶼P恰好在其正北方向，繼續向東航行1小時到達B處，測得島嶼P在其北偏西30°方向，保持航向不變又航行2小時到達C處，此時海監船與島嶼P之間的距離（即PC的長）為（ ）
A. 40海里 B. 60海里 C. 20
海里 D. 40海里
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，橫、縱坐標都是整數的點叫做整點．直線y＝ax與拋物線y＝ax2﹣2ax﹣1（a≠0）圍成的封閉區域（不包含邊界）為W．
（1）求拋物線頂點坐標（用含a的式子表示）；
（2）當a＝
時，寫出區域W內的所有整點坐標；
（3）若區域W內有3個整點，求a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com