
【題目】四邊形![]() 是正方形,
是正方形,![]() 與
與![]() 相交于點
相交于點![]() ,點
,點![]() 、
、![]() 是直線
是直線![]() 上兩動點,且
上兩動點,且![]() ,
,![]() 所在直線與對角線
所在直線與對角線![]() 所在直線交于點
所在直線交于點![]() ,連接
,連接![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() .
.
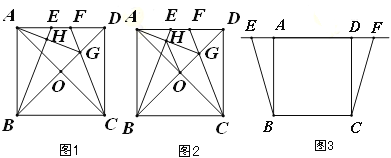
(1)如圖1,當點![]() 、
、![]() 在線段
在線段![]() 上時,
上時,
①求證:![]() ;
;
②猜想![]() 與
與![]() 的位置關系,并加以證明;
的位置關系,并加以證明;
(2)如圖2,在(1)條件下,連接![]() ,試說明
,試說明![]() 平分
平分![]() ;
;
(3)當點![]() 、
、![]() 運動到如圖3所示的位置時,其它條件不變,請將圖形補充完整,并直接寫出
運動到如圖3所示的位置時,其它條件不變,請將圖形補充完整,并直接寫出![]() 的度數.
的度數.
【答案】(1)證明見解析;(2)證明見解析;(3)圖見解析;45°.
【解析】
試題分析:(1)①根據正方形的性質可證DA=DC,∠ADB=∠CDB=45°根據SAS可證△ADG≌△CDG,根據全等三角形的性質可證∠DAG=∠DCG;
②根據正方形的性質可證AB=DC,∠BAD=∠CDA=90°,根據SAS可證△ABE≌△DCF,根據全等三角形的性質可證∠ABE=∠DCF,根據∠DAG+∠BAG=90°可證∠AHB=∠ABE+∠BAG=90°,所以可證AG⊥BE;
(2) 過點O作OM⊥BE于點M,ON⊥AG于點N,則四邊形OMHN為矩形,根據矩形的性質可得:∠AON=∠BOM,∠OAN=∠OBM,根據ASA可證△AON≌△BOM,根據全等三角形的性質可證OM=ON,所以可證矩形OMHN為正方形,根據正方形的性質可證HO平分∠BHG;
(3)圖見解析;根據正方形的性質可證AG⊥BE,過點O作OM⊥BE于點M,ON⊥AG于點N,則可證△AON≌△BOM,根據全等三角形的性質可證OMHN為正方形,所以HO平分∠BHG,所以可證∠BHO=45°.
試題解析:(1)①∵四邊形ABCD為正方形,
∴DA=DC,∠ADB=∠CDB=45°,
在△ADG和△CDG中
 ,
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG;
②AG⊥BE.理由如下:
∵四邊形ABCD為正方形,
∴AB=DC,∠BAD=∠CDA=90°,
在△ABE和△DCF中
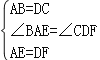 ,
,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
∵∠DAG=∠DCG,
∴∠DAG=∠BAE,
∵∠DAG+∠BAG=90°,
∴∠ABE+∠BAG=90°,
∴∠AHB=90°,
∴AG⊥BE;
(2)由(1)可知AG⊥BE.
如答圖1所示,過點O作OM⊥BE于點M,ON⊥AG于點N,則四邊形OMHN為矩形.
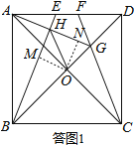
∴∠MON=90°,又∵OA⊥OB,
∴∠AON=∠BOM.
∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,
∴∠OAN=∠OBM.
在△AON與△BOM中,
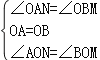
∴△AON≌△BOM(ASA).
∴OM=ON,
∴矩形OMHN為正方形,
∴HO平分∠BHG;
(3)將圖形補充完整,如答圖2示,∠BHO=45°.
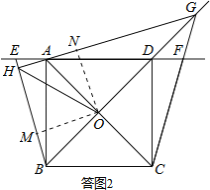
與(1)同理,可以證明AG⊥BE.
過點O作OM⊥BE于點M,ON⊥AG于點N,
與(2)同理,可以證明△AON≌△BOM,
可得OMHN為正方形,
∴HO平分∠BHG,
∴∠BHO=45°.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】下列說法錯誤的是( ).
A. 對角線互相平分的四邊形為平行四邊形
B. 兩組對角分別相等的四邊形為平行四邊形
C. 一組對邊平行且相等的四邊形是平行四邊形
D. 一組對邊平行,另一組對邊相等的四邊形是平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
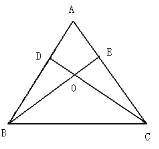
【題目】已知:如圖,銳角△ABC的兩條高BE、CD相交于點O,且OB=OC,
(1)求證:△ABC是等腰三角形;
(2)判斷點O是否在∠BAC的角平分線上,并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝公司招工廣告承諾:熟練工人每月工資至少3000元.每天工作8小時,一個月工作25天.月工資底薪800元,另加計件工資.加工1件![]() 型服裝計酬16元,加工1件
型服裝計酬16元,加工1件![]() 型服裝計酬12元.在工作中發現一名熟練工加工1件
型服裝計酬12元.在工作中發現一名熟練工加工1件![]() 型服裝和2件
型服裝和2件![]() 型服裝需4小時,加工3件
型服裝需4小時,加工3件![]() 型服裝和1件
型服裝和1件![]() 型服裝需7小時.(工人月工資=底薪+計件工資)
型服裝需7小時.(工人月工資=底薪+計件工資)
(1)一名熟練工加工1件![]() 型服裝和1件
型服裝和1件![]() 型服裝各需要多少小時?
型服裝各需要多少小時?
(2)一段時間后,公司規定:“每名工人每月必須加工![]() ,
,![]() 兩種型號的服裝,且加工
兩種型號的服裝,且加工![]() 型服裝數量不少于
型服裝數量不少于![]() 型服裝的一半”.設一名熟練工人每月加工
型服裝的一半”.設一名熟練工人每月加工![]() 型服裝
型服裝![]() 件,工資總額為
件,工資總額為![]() 元.請你運用所學知識判斷該公司在執行規定后是否違背了廣告承諾?
元.請你運用所學知識判斷該公司在執行規定后是否違背了廣告承諾?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列變形屬于因式分解的是( )
A. 4x+x=5xB. (x+2)2=x2+4x+4
C. x2+x+1=x(x+1)+1D. x2﹣3x=x(x﹣3)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com