
【題目】已知,如圖,AB是![]() 的直徑,C是
的直徑,C是![]() 上一點(diǎn),連接AC,過(guò)點(diǎn)C作直線
上一點(diǎn),連接AC,過(guò)點(diǎn)C作直線![]() 于D(
于D(![]() ),點(diǎn)E是DB上任意一點(diǎn)(點(diǎn)D、B除外),直線CE交
),點(diǎn)E是DB上任意一點(diǎn)(點(diǎn)D、B除外),直線CE交![]() 于點(diǎn)F.連接AF與直線CD交于點(diǎn)G.
于點(diǎn)F.連接AF與直線CD交于點(diǎn)G.
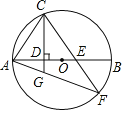

(1)求證:![]()
(2)若點(diǎn)E是AD(點(diǎn)A除外)上任意一點(diǎn),上述結(jié)論是否仍然成立?若成立,請(qǐng)畫出圖形并給予證明;若不成立,請(qǐng)說(shuō)明理由。
【答案】(1)證明見解析;(2)成立,證明見解析.
【解析】
(1)欲證AC2=AGAF,即證AC:AG=AF:AC,可以通過(guò)證明△AGC∽△ACF得到;
(2)分清E點(diǎn)在AD上有兩種情況,然后逐一證明.
(1)證明:連接CB,
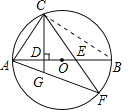
∵AB是直徑,CD⊥AB,
∴∠ACB=∠ADC=90°,又∠CAD=∠BAC,
∴△CAD∽△BAC,
∴∠ACD=∠ABC,
∵∠ABC=∠AFC,
∴∠ACD=∠AFC,∠CAG=∠FAC,
∴△ACG∽△AFC,
∴![]() ,
,
∴AC2=AGAF;
(2)當(dāng)點(diǎn)E是AD(點(diǎn)A除外)上任意一點(diǎn),上述結(jié)論仍成立
①當(dāng)點(diǎn)E與點(diǎn)D重合時(shí),F與G重合,如圖所示:
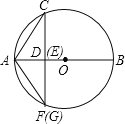
有AG=AF,∵CD⊥AB,
∴![]() ,AC=AF,
,AC=AF,
∴AC2=AGAF;
②當(dāng)點(diǎn)E與點(diǎn)D不重合時(shí)(不含點(diǎn)A)時(shí),如圖所示:
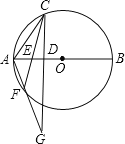
證明類似(1).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是拋物線型拱橋,當(dāng)拱頂離水面2m時(shí),水面寬4m,水面下降2m,水面寬度增加______m.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
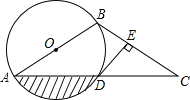
【題目】如圖,以AB為直徑的⊙O經(jīng)過(guò)AC的中點(diǎn)D,DE⊥BC于點(diǎn)E.
(1)求證:DE是⊙O的切線;
(2)當(dāng)AB=4![]() ,∠C=30°時(shí),求圖中陰影部分的面積(結(jié)果保留根號(hào)和π).
,∠C=30°時(shí),求圖中陰影部分的面積(結(jié)果保留根號(hào)和π).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() 是原點(diǎn),矩形
是原點(diǎn),矩形![]() 的頂點(diǎn)
的頂點(diǎn)![]() 在
在![]() 軸的正半軸上,頂點(diǎn)
軸的正半軸上,頂點(diǎn)![]() 在
在![]() 軸的正半軸上,頂點(diǎn)
軸的正半軸上,頂點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,拋物線
,拋物線![]() 經(jīng)過(guò)
經(jīng)過(guò)![]() ,
,![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸的另一個(gè)交點(diǎn)為點(diǎn)
軸的另一個(gè)交點(diǎn)為點(diǎn)![]() .
.
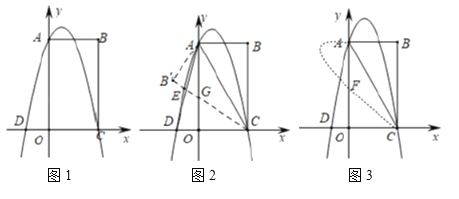
(1)如圖1,求拋物線的函數(shù)表達(dá)式;
(2)如圖2,連接![]() ,
,![]() ,將
,將![]() 沿
沿![]() 折疊后與
折疊后與![]() 、
、![]() 軸分別交于點(diǎn)
軸分別交于點(diǎn)![]() ,
,![]() ,求
,求![]() 的長(zhǎng)度;
的長(zhǎng)度;
(3)如圖3,將拋物線在![]() 上方的部分沿
上方的部分沿![]() 折疊后與
折疊后與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
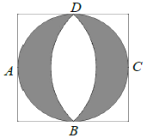
【題目】文藝復(fù)興時(shí)期,意大利藝術(shù)大師達(dá)芬奇曾研究過(guò)圓弧所圍成的許多圖形的面積問(wèn)題. 如圖所示稱為達(dá)芬奇的“貓眼”,可看成圓與正方形的各邊均相切,切點(diǎn)分別為![]() ,
,![]() 所在圓的圓心為點(diǎn)
所在圓的圓心為點(diǎn)![]() (或
(或![]() ). 若正方形的邊長(zhǎng)為2,則圖中陰影部分的面積為( )
). 若正方形的邊長(zhǎng)為2,則圖中陰影部分的面積為( )
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
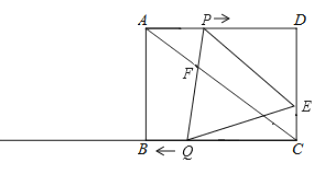
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 向點(diǎn)
向點(diǎn)![]() 勻速運(yùn)動(dòng),速度是
勻速運(yùn)動(dòng),速度是![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,同時(shí),點(diǎn)
,同時(shí),點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 方向,在射線
方向,在射線![]() 上勻速運(yùn)動(dòng),速度是
上勻速運(yùn)動(dòng),速度是![]() ,連接
,連接![]() 、
、![]() ,
,![]() 與
與![]() 交與點(diǎn)
交與點(diǎn)![]() ,設(shè)運(yùn)動(dòng)時(shí)間為
,設(shè)運(yùn)動(dòng)時(shí)間為![]() .
.
(1)當(dāng)![]() 為何值時(shí),四邊形
為何值時(shí),四邊形![]() 是平行四邊形;
是平行四邊形;
(2)設(shè)![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)是否存在某一時(shí)刻![]() ,使得
,使得![]() 的面積為矩形
的面積為矩形![]() 面積的
面積的![]() ;
;
(4)是否存在某一時(shí)刻![]() ,使得點(diǎn)
,使得點(diǎn)![]() 在線段
在線段![]() 的垂直平分線上.
的垂直平分線上.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD中,BD與AC相交于E點(diǎn),AE=CE,BC=AC=DC,則tan∠ABDtan∠ADB=_____.
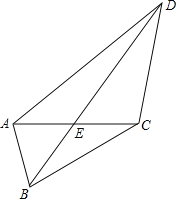
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】現(xiàn)有四張完全相同的不透明卡片,其正面分別寫有數(shù)字-2,-1,0,2,把這四張卡片背面朝上洗勻后放在桌面上.
(1)隨機(jī)抽取一張卡片,求抽取的卡片上的數(shù)字為負(fù)數(shù)的概率;
(2)先隨機(jī)抽取卡片,其上的數(shù)字作為點(diǎn)A的橫坐標(biāo);然后放回并洗勻,再隨機(jī)抽取一張卡片,其上的數(shù)字作為點(diǎn)A的縱坐標(biāo),試用畫樹狀圖或列表的方法求出點(diǎn)A在直線y=2x上的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中點(diǎn)為圓心,OA的長(zhǎng)為半徑作半圓交AC于點(diǎn)D,則圖中陰影部分的面積為( )
,BC=2,以AB的中點(diǎn)為圓心,OA的長(zhǎng)為半徑作半圓交AC于點(diǎn)D,則圖中陰影部分的面積為( )
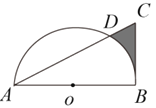
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com