
【題目】我們定義:如圖1,在![]() 中,把AB繞點
中,把AB繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得到
得到![]() ,把AC繞點
,把AC繞點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 得到
得到![]() ,連接
,連接![]() .當
.當![]() 時,我們稱
時,我們稱![]() 是
是![]() 的“旋補三角形”,邊
的“旋補三角形”,邊![]() 上的中線AD叫做
上的中線AD叫做![]() 的“旋補中線”,點A叫做“旋補中心”.
的“旋補中線”,點A叫做“旋補中心”.
特例感知
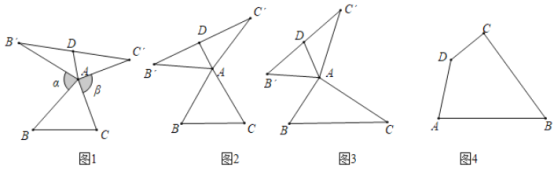
(1)在圖2、圖3中,![]() 是△ABC的“旋補三角形”,
是△ABC的“旋補三角形”,![]() 是的“旋補中線”.
是的“旋補中線”.
①如圖2,當![]() 為等邊三角形時,AD與
為等邊三角形時,AD與![]() 的數量關系為AD=
的數量關系為AD= ![]() ;
;
②如圖3,當![]() 時,則
時,則![]() 長為 .
長為 .
猜想論證
(2)在圖1中,當![]() 為任意三角形時,猜想
為任意三角形時,猜想![]() 與BC的數量關系,并給予證明.
與BC的數量關系,并給予證明.
拓展應用
(3)如圖4,在四邊形![]() 中,
中,![]() .在四邊形內部是否存在點
.在四邊形內部是否存在點![]() ,使
,使![]() 是
是![]() 的“旋補三角形”?若存在,求
的“旋補三角形”?若存在,求![]() 的“旋補中線”長;若不存在,說明理由.
的“旋補中線”長;若不存在,說明理由.
【答案】(1)①![]() ;②4 ;(2)
;②4 ;(2)![]() ,證明見解析;(3)存在,
,證明見解析;(3)存在,![]()
【解析】
(1)①首先證明![]() 是含有30°的直角三角形,可得
是含有30°的直角三角形,可得![]() 即可解決問題;
即可解決問題;
②首先證明![]() ,根據直角三角形斜邊上的中線的性質即可解決問題;
,根據直角三角形斜邊上的中線的性質即可解決問題;
(2)如圖所示作出輔助線,首先證明四邊形![]() 是平行四邊形,再證明
是平行四邊形,再證明![]() ,即可解決問題;
,即可解決問題;
(3)如圖所示作出輔助線,證明PA=PD,PB=PC,再證明∠APD+∠BPC=180°即可.
解:(1)①在圖2中,
∵△ABC是等邊三角形,
∴AB=BC=AC=![]() ,
,
∵![]() ,
,
∴AD⊥![]() ,
,
∵∠BAC=60°,∠BAC+![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案為:![]() ;
;
②在圖3中,
∵∠BAC=90°,∠BAC+![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
故答案為:4;
(2)結論為:![]()
理由:如下圖,延長AD到點M,使得AD=DM,連接![]() ,
,![]() ,
,
∵![]() ,AD=DM,
,AD=DM,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,
∵∠BAC+![]() ,
,![]()
∴![]() ,
,
∵![]()
∴![]() (SAS)
(SAS)
∴BC=AM
∴![]() ;
;
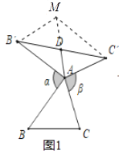
(3)存在,
理由:如圖4中,延長AD交BC的延長線于點M,作BE⊥AD于點E,作線段BC的垂直平分線交BE于點P,交BC于點F,連接PA、PD、PC,作△PCD的中線PN,連接DF交PC于點O.
∵∠ADC=150°,
∴∠MDC=30°,
在Rt△DCM中,
∵![]() ,∠DCM=90°,∠MDC=30°,
,∠DCM=90°,∠MDC=30°,
∴CM=2,DM=4,∠M=60°,
在Rt△BEM中,∵∠BEM=90°,BM=14,∠MBE=30°,
∴EM=![]() ,
,
∴DE=EM-DM=3,
∵AD=6,
∴AE=DE,
∵BE⊥AD,
∴PA=PD,PB=PC,
在Rt△CDF中,∵CD=![]() ,CF=6,
,CF=6,
∴![]() ,
,
∴∠CDF=60°=∠CPF,
∴△FCP≌△CFD,
∴CD=PF,
又∵CD∥PF
∴四邊形CDPF是矩形,
∴∠CDP=90°,
∴∠ADP=∠ADC-∠CDP=60°,
∴△ADP是等邊三角形,
∴∠ADP=60°,
∵∠BPF=∠CPF=60°,
∴∠BPC=120°,
∴∠APD+∠BPC=180°,
∴△PCD是△PAB的“旋補三角形”,
在Rt△PDN中,∵∠PDN=90°,PD=AD=6,DN=![]() ,
,
PN=![]() .
.


科目:初中數學 來源: 題型:
【題目】下列說法:
①一顆質地均勻的骰子已連續拋擲了![]() 次,其中,拋擲出
次,其中,拋擲出![]() 點的次數最少,則第
點的次數最少,則第![]() 次一定拋擲出
次一定拋擲出![]() 點.
點.
②可能性很小的事件在一次實驗中也有可能發生.
③天氣預報說明天下雨的概率是![]() ,意思是說明天將有一半時間在下雨.
,意思是說明天將有一半時間在下雨.
④拋擲一枚圖釘,釘尖觸地和釘尖朝上的概率不相等.
正確的是________(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
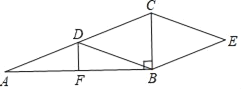
【題目】如圖,Rt△ABC中,∠ABC=90°,點D,F分別是AC,AB的中點,CE∥DB,BE∥DC.
(1)求證:四邊形DBEC是菱形;
(2)若AD=3,DF=1,求四邊形DBEC面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
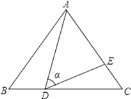
【題目】如圖,在△ABC中,AB=AC=10,點D是邊BC上一動點 (不與B,C重合),∠ADE=∠B=α,DE交AC于點E,且 ![]() .下列結論: ①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8或
.下列結論: ①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8或![]() ;④CD2=CECA.其中正確的結論是________(把你認為正確結論的序號都填上)
;④CD2=CECA.其中正確的結論是________(把你認為正確結論的序號都填上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.
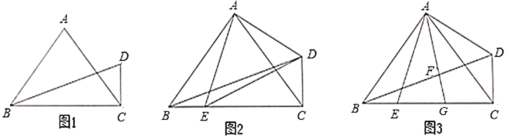
(1)求![]() 的度數:
的度數:
(2)如圖2,連接![]() ,
,![]() 交
交![]() 于
于![]() ,連接
,連接![]() ,求證:
,求證:![]() ;
;
(3)如圖3,在(2)的條件下,點![]() 為
為![]() 的中點,連接
的中點,連接![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的小正方形組成的方格紙中,有一個以格點為頂點的△ABC.
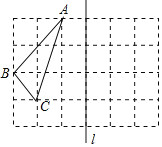
(1)△ABC的形狀是 .
(2)利用網格線畫△A′B′C′,使它與△ABC關于直線l對稱.
(3)在直線l上求作點P使AP+CP的值最小,則AP+CP的最小值= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于點E.
(1)求∠E的度數.
(2)請猜想∠A與∠E之間的數量關系,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com