Question

一家商店進行裝修，若請甲、乙兩個裝修組同時施工，8天可以完成，需付給兩組費用共3520元；若先請甲組單獨做6天，再請乙組單獨做12天可以完成，需付給兩組費用共3480元，問：

（1）甲、乙兩組單獨工作一天，商店應各付多少元？

（2）已知甲組單獨完成需要12天，乙組單獨完成需要24天，單獨請哪組，商店此付費用較少？

（3）若裝修完后，商店每天可盈利200元，你認為如何安排施工有利用商店經營？說說你的理由。（可以直接用（1）（2）中的已知條件）

Answer 1

（1）設甲單獨做一天商店應付x元，乙單獨做一天商店應付y元。依題意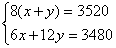 得：   解得：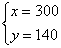

（2）請甲組單獨做需付款300×12＝3600元，請乙組單獨做需付款140×24＝3360元，因為3600＞3360，所以請乙組單獨做，商店應付費用較少。

（3）由（2）知：①甲組單獨做12天完成，需付款3600元，乙組單獨做24天完成，需付款3360元，由于甲組裝修完比乙組裝修完商店早開張12天，12天可以盈利200×12＝2400元，即選擇甲組裝修相當只付裝修費用1200元，所以選擇甲單獨做比選擇已單獨做合算。

②由（1）知，甲、乙同時做需8天完成，需付款3520元又比甲組單獨做少用4天，4天可以盈利200×4＝800元，3520－800＝2720元，這個數字又比甲單獨做12天用3600元和算。

綜上所述，選擇甲、乙兩組合做8天的方案最佳。