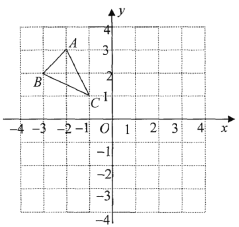
【題目】△ABC在平面直角坐標系中的位置如圖所示.
（1）將△ABC向下平移3個單位長度，再向右平移2個單位長度，畫出平移后的△A1B1C1；并寫出頂點A1、B1、C1各點的坐標；
（2）計算△A1B1C1的面積。
科目：初中數學 來源： 題型：
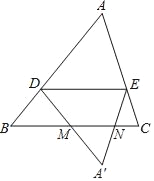
【題目】如圖，在△ABC中，點D在邊AB上（不與A，B重合），DE∥BC交AC于點E，將△ADE沿直線DE翻折，得到△A′DE，直線DA′，EA′分別交直線BC于點M，N．
（1）求證：DB=DM．
（2）若
=2，DE=6，求線段MN的長．
（3）若
=n（n≠1），DE=a，則線段MN的長為 （用含n的代數式表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
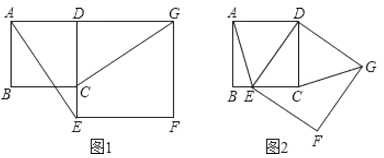
【題目】如圖1，已知正方形ABCD的邊CD在正方形DEFG的邊DE上，連接AE、GC．
（1）試猜想AE與GC有怎樣的關系，并證明你的結論．
（2）將正方形DEFG繞點D按順時針方向旋轉，使點E落在BC邊上，如圖2，連接AE和CG．你認為（1）中的結論是否還成立？若成立，給出證明；若不成立，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】四邊形ABCD中，AD∥BC，要判別四邊形ABCD是平行四邊形，還需滿足條件（ ）
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一次函數y=ax+b（a≠0）、二次函數y=ax2+bx和反比例函數y=
（k≠0）在同一直角坐標系中的圖象如圖所示，A點的坐標為（-2，0），則下列結論中，正確的是（ ）
A．b=2a+k B．a=b+k C．a＞b＞0 D．a＞k＞0
查看答案和解析>>
科目：初中數學 來源： 題型：
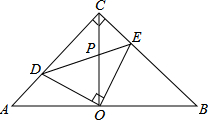
【題目】如圖，在等腰直角△ABC中，∠ACB=90°，O是斜邊AB的中點，點D，E分別在直角邊AC，BC上，且∠DOE=90°，DE交OC于點P．則下列結論：(1)AD+BE=AC；(2)AD2+BE2=DE2；(3)△ABC的面積等于四邊形CDOE面積的2倍；(4)OD=OE．其中正確的結論有( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，∠B=90°，AD//BC，AD=16，BC=21，CD=13．
（1）求直線AD和BC之間的距離；
（2）動點P從點B出發，沿射線BC以每秒2個單位長度的速度運動，動點Q從點A出發，在線段AD上以每秒1個單位長度的速度運動，點P、Q同時出發，當點Q運動到點D時，兩點同時停止運動，設運動時間為t秒．試求當t為何值時，以P、Q、D、C為頂點的四邊形為平行四邊形？
（3）在（2）的條件下，是否存在點P，使△PQD為等腰三角形？若存在，請直接寫出相應的t值，若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
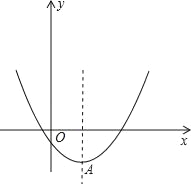
【題目】已知二次函數y=x2﹣2mx+4m﹣8,
（1）當x≤2時，函數值y隨x的增大而減小，求m的取值范圍．
（2）以拋物線y=x2﹣2mx+4m﹣8的頂點A為一個頂點作該拋物線的內接正三角形AMN（M，N兩點在拋物線上），請問：△AMN的面積是與m無關的定值嗎？若是，請求出這個定值；若不是，請說明理由．
（3）若拋物線y=x2﹣2mx+4m﹣8與x軸交點的橫坐標均為整數，求整數m的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是計算機中的一種益智小游戲“掃雷”的畫面，在一個9×9的小方格的正方形雷區中，隨機埋藏著10顆地雷，每個小方格內最多只能埋藏1顆地雷。
小紅在游戲開始時首先隨機地點擊一個方格,該方格中出現了數字“3”,其意義表示該格的外圍區域(圖中陰影部分,記為A區域)有3顆地雷;接著,小紅又點擊了左上角第一個方格,出現了數字“1”,其外圍區域(圖中陰影部分)記為B區域；“A區域與B區域以及出現數字‘1’和‘3’兩格”以外的部分記為C區域。小紅在下一步點擊時要盡可能地避開地雷，那么她應點擊A. B. C中的哪個區域?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
