
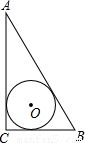
 (AC+BC-AB),由此可求出r的長.
(AC+BC-AB),由此可求出r的長. 解:如圖;
解:如圖; =5;
=5; (AC+BC-AB);
(AC+BC-AB); (3+4-5)=1.
(3+4-5)=1. (AC+BC-AB)是解題關鍵.
(AC+BC-AB)是解題關鍵. 

 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
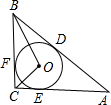 如圖,⊙O內切于Rt△ABC,∠C=Rt∠,D、E、F是切點,若∠BOC=105°,AB=4cm,則∠OBC=
如圖,⊙O內切于Rt△ABC,∠C=Rt∠,D、E、F是切點,若∠BOC=105°,AB=4cm,則∠OBC=查看答案和解析>>
科目:初中數學 來源:《24.2 與圓有關的位置關系》2010年同步練習1(解析版) 題型:填空題

查看答案和解析>>
科目:初中數學 來源:同步題 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com