
【題目】如圖①所示,已知正方形ABCD和正方形AEFG,連接DG,BE.

(1)發現:當正方形AEFG繞點A旋轉,如圖②所示.
①線段DG與BE之間的數量關系是 ;
②直線DG與直線BE之間的位置關系是 ;
(2)探究:如圖③所示,若四邊形ABCD與四邊形AEFG都為矩形,且AD=2AB,AG=2AE時,上述結論是否成立,并說明理由.
(3)應用:在(2)的情況下,連接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接寫出結果).
【答案】(1)①BE=DG,②BE⊥DG;(2)數量關系不成立,DG=2BE,位置關系成立.理由見解析;(3)BG2+DE2=25.
【解析】
(1)先判斷出△ABE≌△DAG,進而得出BE=DG,∠ABE=∠ADG,再利用等角的余角相等即可得出結論;
(2)先利用兩邊對應成比例夾角相等判斷出△ABE∽△DAG,得出∠ABE=∠ADG,再利用等角的余角相等即可得出結論;
(3)如圖④中,作ET⊥AD于T,GH⊥BA交BA的延長線于H.設ET=x,AT=y.利用勾股定理,以及相似三角形的性質即可解決問題.
(1)①如圖②中,
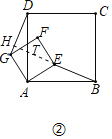
∵四邊形ABCD和四邊形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△DAG中,
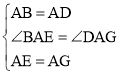 ,
,
∴△ABE≌△DAG(SAS),
∴BE=DG;
②如圖2,延長BE交AD于T,交DG于H.
由①知,△ABE≌△DAG,
∴∠ABE=∠ADG,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG,
故答案為:BE=DG,BE⊥DG;
(2)數量關系不成立,DG=2BE,位置關系成立.
如圖③中,延長BE交AD于T,交DG于H.
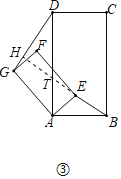
∵四邊形ABCD與四邊形AEFG都為矩形,
∴∠BAD=∠DAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴![]() =
=![]() =
=![]() ,
,
∴△ABE∽△ADG,
∴∠ABE=∠ADG,![]() =
=![]() ,
,
∴DG=2BE,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如圖④中,作ET⊥AD于T,GH⊥BA交BA的延長線于H.設ET=x,AT=y.
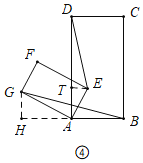
∵∠GAH+∠DAG=90°,∠BAE+∠DAG=90°,
∴∠GAH=∠BAE,
又∵∠GHA=∠ATE=90°,
∴△AHG∽△ATE,
∴![]() =2,
=2,
∴GH=2x,AH=2y,
∴4x2+4y2=4,
∴x2+y2=1,
∴BG2+DE2=(2x)2+(2y+2)2+x2+(4﹣y)2=5x2+5y2+20=25.


科目:初中數學 來源: 題型:
【題目】某市少年宮為小學生開設了繪畫、音樂、舞蹈和跆拳道四類興趣班,為了解學生對這四類興趣班的喜愛情況,對學生進行了隨機問卷調查(問卷調查表如圖所示),將調查結果整理后繪制了一幅不完整的統計表
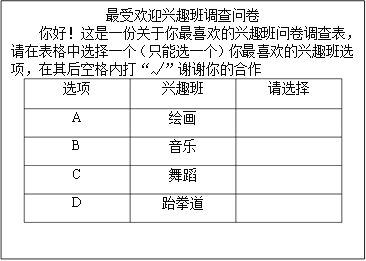
興趣班 | 頻數 | 頻率 |
A | 0.35 | |
B | 18 | 0.30 |
C | 15 |
|
D | 6 | |
合計 |
| 1 |
請你根據統計表中提供的信息回答下列問題:
(1)統計表中的![]() ,
,![]() ;
;
(2)根據調查結果,請你估計該市2000名小學生中最喜歡“繪畫”興趣的人數;
(3)王姝和李要選擇參加興趣班,若他們每人從![]() 、
、![]() 、
、![]() 、
、![]() 四類興趣班中隨機選取一類,請用畫樹狀圖或列表格的方法,求兩人恰好選中同一類的概率.
四類興趣班中隨機選取一類,請用畫樹狀圖或列表格的方法,求兩人恰好選中同一類的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,我們不妨把橫坐標和縱坐標相等的點叫“相等點”,例如點![]() ,
,![]()
![]() 都是“相等點”,顯然“相等點”有無數個.
都是“相等點”,顯然“相等點”有無數個.
(1)若點![]() 是反比例函數
是反比例函數![]() 為常數,
為常數,![]() )的圖象上的“相等點”,求這個反比例函數的解析式;
)的圖象上的“相等點”,求這個反比例函數的解析式;
(2)一次函數![]() 為常數,
為常數,![]() )的圖象上存在“相等點”嗎?若存在,請用含
)的圖象上存在“相等點”嗎?若存在,請用含![]() 的式子表示出“相等點”的坐標,若不存在,說明理由;
的式子表示出“相等點”的坐標,若不存在,說明理由;
(3)若二次函數![]() 為常數)的圖象上有且只有一個“相等點”,令
為常數)的圖象上有且只有一個“相等點”,令![]() 當
當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
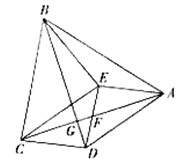
【題目】如圖,四邊形ABCD內一點E滿足EB=EC,EA=ED,∠BEC=∠AED=90°,AC交DE于點F,交BD于點G.
(1)∠AGB的度數為
(2)若四邊形AECD是平行四邊形
①求證:AC=AB
②若AE=2,求AF·CG的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為創建全國文明城市,開展“美化綠化城市”活動,計劃經過若干年使城區綠化總面積新增![]() 萬平方米.自
萬平方米.自![]() 年初開始實施后,實際每年綠化面積是原計劃的
年初開始實施后,實際每年綠化面積是原計劃的![]() 倍,這樣可提前
倍,這樣可提前![]() 年完成任務.
年完成任務.
(1)問實際每年綠化面積多少萬平方米?
(2)為加大創城力度,市政府決定從![]() 年起加快綠化速度,要求不超過
年起加快綠化速度,要求不超過![]() 年完成,那么實際平均每年綠化面積至少還要增加多少萬平方米?
年完成,那么實際平均每年綠化面積至少還要增加多少萬平方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
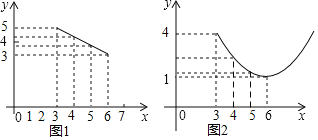
【題目】某種蔬菜每千克售價y1(元)與銷售月份x之間的關系如圖1所示,每千克成本y2(元)與銷售月份x之間的關系如圖2所示,其中圖1中的點在同一條線段上,圖2中的點在對稱軸平行于y軸的同一條拋物線上,且拋物線的最低點的坐標為(6,1).
(1)求出y1與x函數關系式;
(2)求出y2與x函數關系式;
(3)設這種蔬菜每千克收益為w元,試問在哪個月份出售這種蔬菜,w將取得最大值?并求出此最大值.(收益=售價﹣成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
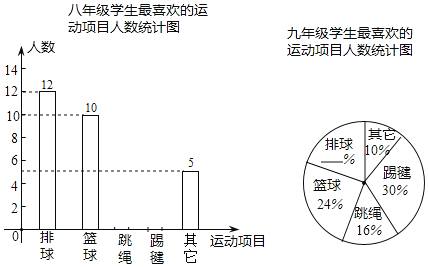
【題目】通遼市某中學為了了解學生“大課間”活動情況,在七、八、九年級的學生中,分別抽取了相同數量的學生對“你最喜歡的運動項目”進行調查(每人只能選一項),調查結果的部分數據如下表(圖)所示,其中七年級最喜歡跳繩的人數比八年級多5人,九年級最喜歡排球的人數為10人.
七年級學生最喜歡的運動項目人數統計表
項目 | 排球 | 籃球 | 踢毽 | 跳繩 | 其他 |
人數(人) | 7 | 8 | 14 |
| 6 |
請根據以上統計表(圖)解答下列問題:
(1)本次調查共抽取了多少人?
(2)補全統計表和統計圖.
(3)該校有學生1800人,學校想對“最喜歡踢毽子”的學生每4人提供一個毽子,學校現有124個毽子,能否夠用?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場準備采購一批特色商品,經調查,用5000元采購![]() 型商品的件數是用2000元采購
型商品的件數是用2000元采購![]() 型商品的件數的2倍,一件
型商品的件數的2倍,一件![]() 型商品的進價比一件
型商品的進價比一件![]() 型商品的進價多10元.
型商品的進價多10元.
(1)求一件![]() ,
,![]() 型商品的進價分別為多少元?
型商品的進價分別為多少元?
(2)若該商場購進![]() ,
,![]() 型商品共200件進行試銷,其中
型商品共200件進行試銷,其中![]() 型商品的件數不大于
型商品的件數不大于![]() 型商品的件數,且不小于80件.已知
型商品的件數,且不小于80件.已知![]() 型商品的售價為80元/件,
型商品的售價為80元/件,![]() 型商品的售價為60元/件,且
型商品的售價為60元/件,且![]() ,
,![]() 型商品均全部售出.設購進
型商品均全部售出.設購進![]() 型商品
型商品![]() 件,求該商場銷售完這批商品的利潤
件,求該商場銷售完這批商品的利潤![]() 與
與![]() 之間的函數關系式,并寫出
之間的函數關系式,并寫出![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,商場決定在試銷活動中每售出一件![]() 型商品,就從一件
型商品,就從一件![]() 型商品的利潤中捐獻慈善資金
型商品的利潤中捐獻慈善資金![]() 元
元![]() ,若該商場售完
,若該商場售完![]() 、
、![]() 型所有商品并捐獻資金后獲得的最大收益是4800元,求出
型所有商品并捐獻資金后獲得的最大收益是4800元,求出![]() 值.
值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com