
【題目】拋物線y=-2x+mx+n經過點A(0,2),B(3,-4).
(1)求該拋物線的函數表達式及對稱軸;
(2)設點B關于原點的對稱點為C,點D是拋物線對稱軸上一動點,記拋物線在A,B之間的部分為圖象G(包含A,B兩點),如果直線CD與圖象G有兩個公共點,結合函數的圖象,求點D縱坐標t的取值范圍.
【答案】(1)y=-2x+4x+2,對稱軸為直線x=1;(2)t的范圍為![]() ≤t<4
≤t<4
【解析】
(1)根據待定系數法求出二次函數的解析式,根據公式得到對稱軸的解析式即可;
(2)求出點C的坐標以及以及二次函數的最大值,求出AC與對稱軸的交點即可得到t的范圍.
(1)解:拋物線y=-2x+bx+c經過點A(0,2),B(3,-4),代入得
![]() 解得:
解得:![]()
∴拋物線的表達式為y=-2x+4x+2,
對稱軸為直線x=1
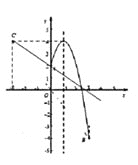
(2)解:由題意得C(-3,4),
當x=1時,y=4
所以二次函數y=-2x+4x+2的最大值為4.
由函數圖象得出D縱坐標最大值為4
設直線AC的表達式為y=kx+b
把A和點C的坐標代入得:
![]()
解得
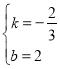
∴直線AC的表達式為y=![]() x+2
x+2
當x=1時,y=![]()
∴t的范圍為![]() ≤t<4
≤t<4


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
【題目】某小區游泳館夏季推出兩種收費方式.方式一:先購買會員證,會員證200元,只限本人當年使用,憑證游泳每次需另付費10元:方式二:不購買會員證,每次游泳需付費20元.
(1)若甲計劃今年夏季游泳的費用為500元,則選擇哪種付費方式游泳次數比較多?
(2)若乙計劃今年夏季游泳的次數超過15次,則選擇哪種付費方式游泳花費比較少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=-x2+bx+c經過點A(3,0)和點B(2,3),過點A的直線與y軸的負半軸相交于點C,且tan∠CAO=![]() .
.
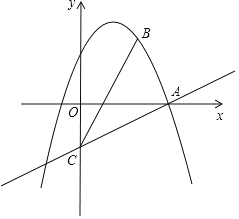
(1)求這條拋物線的表達式及對稱軸;
(2)聯結AB、BC,求∠ABC的正切值;
(3)若點D在x軸下方的對稱軸上,當S△DBC=S△ADC時,求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】參照學習函數的過程方法,探究函數![]() 的圖像與性質,因為
的圖像與性質,因為![]() ,即
,即![]() ,所以我們對比函數
,所以我們對比函數![]() 來探究列表:
來探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描點:在平面直角坐標系中以自變量![]() 的取值為橫坐標,以
的取值為橫坐標,以![]() 相應的函數值為縱坐標,描出相應的點如圖所示:
相應的函數值為縱坐標,描出相應的點如圖所示:
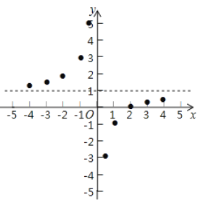
(1)請把![]() 軸左邊各點和右邊各點分別用一條光滑曲線,順次連接起來;
軸左邊各點和右邊各點分別用一條光滑曲線,順次連接起來;
(2)觀察圖象并分析表格,回答下列問題:
①當![]() 時,
時,![]() 隨
隨![]() 的增大而______;(“增大”或“減小”)
的增大而______;(“增大”或“減小”)
②![]() 的圖象是由
的圖象是由![]() 的圖象向______平移______個單位而得到的;
的圖象向______平移______個單位而得到的;
③圖象關于點______中心對稱.(填點的坐標)
(3)函數![]() 與直線
與直線![]() 交于點
交于點![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=2x與函數y=![]() (x>0)的圖象交于點A(1,2).
(x>0)的圖象交于點A(1,2).
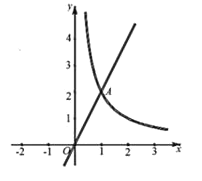
(1)求m的值;
(2)過點A作x軸的平行線l,直線y=2x+b與直線l交于點B,與函數y=![]() (x>0)的圖象交于點C,與x軸交于點D.
(x>0)的圖象交于點C,與x軸交于點D.
①若點C是線段BD的中點時,則點C的坐標是________,b的值是________;
②當BC>BD時,直接寫出b的取值范圍________.
查看答案和解析>>
科目:初中數學 來源: 題型:
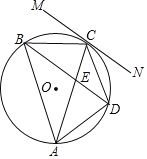
【題目】如圖,⊙O為△ABC的外接圓,直線MN與⊙O相切于點C,弦BD∥MN,AC與BD相交于點E.
(1)求證:∠CAB=∠CBD;
(2)若BC=5,BD =8,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 的頂點
的頂點![]() 、
、![]() 分別在
分別在![]() 軸,
軸,![]() 軸上,頂點
軸上,頂點![]() 在第二象限,點
在第二象限,點![]() 的坐標為
的坐標為![]() .將線段
.將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 至線段
至線段![]() ,若反比例函數y=
,若反比例函數y=![]() (k≠0)的圖象經過A、D兩點,則k值為_________.
(k≠0)的圖象經過A、D兩點,則k值為_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
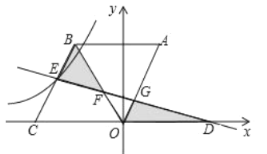
【題目】如圖菱形![]() 中,
中,![]() ,點C坐標
,點C坐標![]() ,過點
,過點![]() 作直線
作直線![]() 分別交
分別交![]() 于點
于點![]() ,交
,交![]() 于E,點E在反比例函數
于E,點E在反比例函數![]() 的圖象上,若
的圖象上,若![]() 和
和![]() (即圖中兩陰影部分)的面積相等,則
(即圖中兩陰影部分)的面積相等,則![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
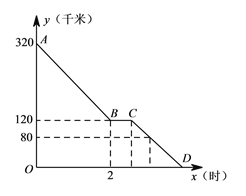
【題目】上周六上午![]() 點,小穎同爸爸媽媽一起從西安出發回安康看望姥姥,途中他們在一個服務區休息了半小時,然后直達姥姥家,如圖,是小穎一家這次行程中距姥姥家的距離
點,小穎同爸爸媽媽一起從西安出發回安康看望姥姥,途中他們在一個服務區休息了半小時,然后直達姥姥家,如圖,是小穎一家這次行程中距姥姥家的距離![]() (千米)與他們路途所用的時間
(千米)與他們路途所用的時間![]() (時)之間的函數圖象,請根據以上信息,解答下列問題:
(時)之間的函數圖象,請根據以上信息,解答下列問題:
(1)求直線![]() 所對應的函數關系式;
所對應的函數關系式;
(2)已知小穎一家出服務區后,行駛![]() 分鐘時,距姥姥家還有
分鐘時,距姥姥家還有![]() 千米,問小穎一家當天幾點到達姥姥家?
千米,問小穎一家當天幾點到達姥姥家?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com