
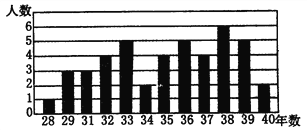
【題目】菲爾茲獎(The International Medals for Outstanding Discoveries in Mathematics)是國際數學聯盟的國際數學家大會上頒發的獎項。每四年一次頒給有卓越貢獻的年輕數學家,得獎者須在該年元旦前未滿四十歲。菲爾茲獎被視為數學界的諾貝爾獎。本題中給出的條形圖是截止到2002年44位費爾茲獎得主獲獎時的年齡統計圖。經計算菲爾茲獎得主獲獎時的平均年齡是35歲。請根據條形圖回答問題:
(1)費爾茲獎得主獲獎時的年齡超過中位數的有多少人?
(2)費爾茲獎得主獲獎時年齡的眾數是多少?
(3)費爾茲獎得主獲獎時的年齡高于平均年齡的人數占獲獎人數的百分比是多少?
【答案】(1)中位數為35.5歲,年齡超過中位數的有22人;(2)眾數是38歲;(3)50%.
【解析】試題分析:(1)把條形統計圖中所給的數據按從小到大的順序排列,根據中位數的定義計算出這組數據的中位數,即可求得費爾茲獎得主獲獎時的年齡超過中位數的人數;(2)根據眾數是一組數據中出現次數最多的數據,即可得這組數據的眾數,注意眾數可以不止一個;(3)高于平均年齡35的人數為22人,即可求得費爾茲獎得主獲獎時的年齡高于平均年齡的人數占獲獎人數的百分比.
試題解析:
(1)∵中位數為35.5歲,
∴年齡超過中位數的有22人.
(2) 眾數是38歲;
(3)高于平均年齡的人數為22人,
22÷44=50%
∴費爾茲獎得主獲獎時的年齡高于平均年齡的人數占獲獎人數的百分比是50%.


科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.動點M從點B出發,在BA邊上以每秒3cm的速度向定點A運動,同時動點N從點C出發,在CB邊上以每秒2cm的速度向點B運動,運動時間為t秒(0<t<![]() ),連接MN.
),連接MN.
(1)若△BMN與△ABC相似,求t的值;
(2)連接AN,CM,若AN⊥CM,求t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如圖1,點D,E在AB,AC上,則BD,CE滿足怎樣的數量關系和位置關系?(直接寫出答案)
(2)如圖2,點D在△ABC內部, 點E在△ABC外部,連結BD, CE, 則BD,CE滿足怎樣的數量關系和位置關系?請說明理由.
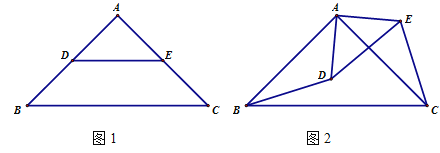
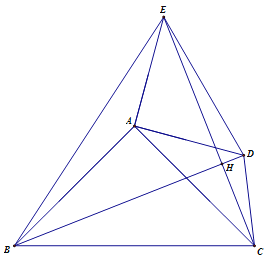
(3)如圖3,點D,E都在△ABC外部,連結BD, CE, CD, EB,BD, 與CE相交于H點.
①若BD=![]() ,求四邊形BCDE的面積;
,求四邊形BCDE的面積;
②若AB=3,AD=2,設CD2=x,EB2=y,求y與x之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次測驗中,某學習小組5名學生成績如下(單位:分):68 、75、67、66、99.這組成績的平均分![]() =____________中位數M= ___________;若去掉一個最高分后的平均分
=____________中位數M= ___________;若去掉一個最高分后的平均分![]() =_____________;那么所求的
=_____________;那么所求的![]() ,M,
,M,![]() 這三個數據中,你認為能描述該小組學生這次測驗成績的一般水平的數據是________________.
這三個數據中,你認為能描述該小組學生這次測驗成績的一般水平的數據是________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:①9-1=8,②16-4=12,③25-9=16,④36-16=20,…寫出第10個等式________________:,第n(n≥1)個式子是________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列去括號正確的是( )
A. ﹣3(b﹣1)=﹣3b﹣3B. 2(2﹣a)=4﹣a
C. ﹣3(b﹣1)=﹣3b+3D. 2(2﹣a)=2a﹣4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com