
【題目】如圖,在△ABC中,∠A=90°,O是BC邊上一點,以O為圓心的半圓分別與AB、AC邊相切于D、E兩點,連接OD.已知BD=2,AD=3.求: 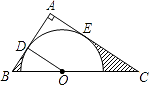
(1)tanC;
(2)圖中兩部分陰影面積的和.
【答案】
(1)解:連接OE,
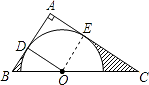
∵AB、AC分別切⊙O于D、E兩點,
∴AD⊥OD,AE⊥OE,
∴∠ADO=∠AEO=90°,
又∵∠A=90°,
∴四邊形ADOE是矩形,
∵OD=OE,
∴四邊形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中, ![]() ,
,
∴ ![]() .
.
答:tanC= ![]()
(2)解:如圖,設⊙O與BC交于M、N兩點,
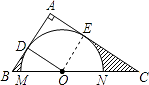
由(1)得:四邊形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中, ![]() =
= ![]() ,OE=3,
,OE=3,
∴ ![]() ,
,
∴S扇形DOM+S扇形EON=S扇形DOE= ![]() ,
,
∴S陰影=S△BOD+S△COE﹣(S扇形DOM+S扇形EON)= ![]() ,
,
答:圖中兩部分陰影面積的和為 ![]() .
.
【解析】(1)連接OE,得到∠ADO=∠AEO=90°,根據∠A=90°,推出矩形ADOE,進一步推出正方形ADOE,得出OD∥AC,OD=AD=3,∠BOD=∠C,即可求出答案;(2)設⊙O與BC交于M、N兩點,由(1)得:四邊形ADOE是正方形,推出∠COE+∠BOD=90°,根據 ![]() ,OE=3,求出
,OE=3,求出 ![]() ,根據S扇形DOM+S扇形EON=S扇形DOE , 即可求出陰影部分的面積.
,根據S扇形DOM+S扇形EON=S扇形DOE , 即可求出陰影部分的面積.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數學 來源: 題型:
【題目】小華和小容都想參加學校組織的數學興趣小組,根據學校分配的名額,他們兩人只能有1人參加.數學老師想出了一個主意:如圖,給他們六張卡片,每張卡片上都有一些數,將化簡后的數在數軸上表示出來,再用“<”連接起來,誰先按照要求做對,誰就參加興趣小組,你也一起來試一試吧!
-(-2) (-1)3 -|-3| 0的相反數
① ② ③ ④
-0.4的倒數 比-1大2.5的數
⑤ ⑥
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某村莊計劃建造A,B兩種型號的沼氣池共20個,以解決該村所有農戶的燃料問題.兩種型號沼氣池的占地面積和可供使用農戶數見下表:
型號 | 占地面積 (單位:m2/個) | 可供使用農戶數 (單位:戶/個) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼氣池的占地面積不超過365m2,該村農戶共有492戶.
(1)如何合理分配建造A,B型號“沼氣池”的個數才能滿足條件?滿足條件的方案有幾種?通過計算分別寫出各種方案.
(2)請寫出建造A、B兩種型號的“沼氣池”的總費用y和建造A型“沼氣池”個數x之間的函數關系式;
(3)若A型號“沼氣池”每個造價2萬元,B型號“沼氣池”每個造價3萬元,試說明在(1)中的各種建造方案中,哪種建造方案最省錢,最少的費用需要多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某七年級的同學就“別人幫助你時,你是否會道一聲謝謝”這個問題對本班級66名同學進行了調查,調查結果如下:
是 是 是 有時 是 是 是 否 是 有時 有時 是 是 有時 有時 是 是 有時 是 是 有時 有時 是 有時 是 是 有時 有時 有時 是 是 是 有時 有時 否 否 有時 有時 是 是 否 是 是 是 否 是 是 是 是 是 是 是 是 有時 是 否 是 是 是 是 否 否 否 是 否 是
(1)請用統計表整理上述數據,百分比的結果精確到整數.
回答內容 | 劃記 | 人數 | 百分比 |
是 | |||
有時 | |||
否 |
(2)通過對這組數據的分析,你有何感想?用一句話表示即可.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC繞頂點C逆時針旋轉得到△A′B′C′,且點B剛好落在A′B′上,若∠A=25°,∠BCA′=45°,則∠A′BA等于( )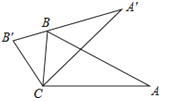
A.30°
B.35°
C.40°
D.45°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在ABCD中,點E在AD上,連接BE,DF∥BE交BC于點F,AF與BE交于點M,CE與DF交于點N,AF,BE分別平分∠BAD,∠ABC;CE,DF分別平分∠BCD,∠ADC,則四邊形MFNE是( )

A. 菱形 B. 矩形 C. 平行四邊形 D. 正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是正方形,對角線AC,BD相交于點O.
(1)如圖1,點P是正方形ABCD外一點,連接OP,以OP為一邊,作正方形OPMN,且邊ON與邊BC相交,連接AP,BN.
①依題意補全圖1;
②判斷AP與BN的數量關系及位置關系,寫出結論并加以證明;
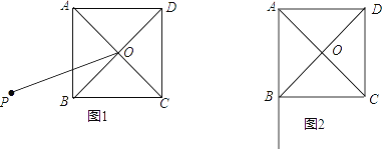
(2)點P在AB延長線上,且∠APO=30°,連接OP,以OP為一邊,作正方形OPMN,且邊ON與BC的延長線恰交于點N,連接CM,若AB=2,求CM的長(不必寫出計算結果,簡述求CM長的過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小王購買了一套一居室,他準備將房子的地面鋪上地磚,地面結構如圖所示,根據圖中所給的數據(單位:米),解答下列問題:
(1)用含 ![]() 的代數式表示地面的總面積
的代數式表示地面的總面積 ![]() ;
;

(2)已知 ![]() ,且客廳面積是衛生間面積的
,且客廳面積是衛生間面積的 ![]() 倍,如果鋪
倍,如果鋪 ![]() 平方米地磚的平均費用為
平方米地磚的平均費用為 ![]() 元,那么小王鋪地磚的總費用為多少元?
元,那么小王鋪地磚的總費用為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com