
【題目】小亮在研究矩形的面積S與矩形的邊長x,y之間的關系時,得到下表數據:
x | 0.5 | 1 | 1.5 | 2 | 3 | 4 | 6 | 12 |
y | 12 | 6 | ■ | 3 | 2 | 1.5 | 1 | 0.5 |
結果發現一個數據被墨水涂黑了.
(1)被墨水涂黑的數據為_________;
(2)y與x的函數關系式為_________,且y隨x的增大而_________;
(3)如圖是小亮畫出的y關于x的函數圖象,點B、E均在該函數的圖象上,其中矩形![]() 的面積記為
的面積記為![]() ,矩形
,矩形![]() 的面積記為
的面積記為![]() ,請判斷
,請判斷![]() 與
與![]() 的大小關系,并說明理由;
的大小關系,并說明理由;
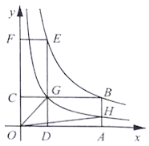
(4)在(3)的條件下,![]() 交
交![]() 于點G,反比例函數
于點G,反比例函數![]() 的圖象經過點G交
的圖象經過點G交![]() 于點H,連接
于點H,連接![]() 、
、![]() ,則四邊形
,則四邊形![]() 的面積為_________.
的面積為_________.
【答案】(1)4;(2)y=![]() ,減小;(3)
,減小;(3)![]() ,說明見解析;(4)4
,說明見解析;(4)4
【解析】
(1)矩形的面積S=xy,先根據表格中的數據得出S的值,然后確定涂黑處的值;
(2)y=![]() ,第(1)問中已經求出S的值,可得x、y的函數關系,根據反比例函數的增減性,可得y隨x的變化情況;
,第(1)問中已經求出S的值,可得x、y的函數關系,根據反比例函數的增減性,可得y隨x的變化情況;
(3)根據反比例函數k的幾何意義可得![]() 與
與![]() 的大小關系;
的大小關系;
(4)如下圖,依據反比例函數k的幾何意義,可知![]() ,從而得出
,從而得出![]() .
.
(1)∵表格中x、y表示矩形的邊長
則S=xy=0.5![]() ,解得:S=6
,解得:S=6
∴當x=1.5時,y=4;
(2)∵S=xy=6
∴y=![]()
根據反比例函數的性質,在第一象限內,y隨x的增大而減小;
(3)∵y=![]()
其中k=6表示任取函數圖像上一點P,過點分別做x軸、y軸垂線,則與坐標軸構成的矩形面積為6
∴![]() ,
,![]()
∴![]() ;
;
(4)如下圖,ED與OH交于點M

反比例函數k的幾何意義還可以如下圖,表示為:任取函數上一點P,向x軸作垂線,交x軸于點N,則△ONP的面積為![]()

∵點G在![]() 函數圖像上
函數圖像上
∴![]() =
=![]() =1
=1
∴![]()
∴![]() .
.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() 經過點
經過點![]() ,對稱軸是直線
,對稱軸是直線![]() ,頂點為點
,頂點為點![]() ,拋物線與
,拋物線與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線的表達式和點![]() 的坐標;
的坐標;
(2)將上述拋物線向下平移![]() 個單位,平移后的拋物線與
個單位,平移后的拋物線與![]() 軸正半軸交于點
軸正半軸交于點![]() ,求
,求![]() 的面積;
的面積;
(3)如果點![]() 在原拋物線上,且在對稱軸的右側,聯結
在原拋物線上,且在對稱軸的右側,聯結![]() 交線段
交線段![]() 于點
于點![]() ,
,![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
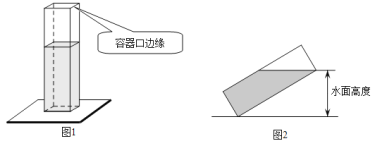
【題目】如圖1,長、寬均為3,高為8的長方體容器,放置在水平桌面上,里面盛有水,水面高為6,繞底面一棱長進行旋轉傾斜后,水面恰好觸到容器口邊緣,圖2是此時的示意圖,則圖2中水面高度為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初級中學數學興趣小組為了解本校學生年齡情況,隨機調查了本校部分學生的年齡,根據所調查的學生的年齡(單位:歲),繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題:

(1)本次接受調查的學生人數為_______,圖①中 ![]() 的值為 ;
的值為 ;
(2)求統計的這組學生年齡數據的平均數、眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
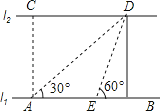
【題目】如圖,河的兩岸l1與l2互相平行,A、B是l1上的兩點,C、D是l2上的兩點,某同學在A處測得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到達點E(即AE=20),測得∠DEB=60°.求:C,D兩點間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖拋物線![]() 與坐標軸分別交于點
與坐標軸分別交于點![]() ,
,![]() ,
,![]() ,點P是線段AB上方的拋物線上的一個動點.
,點P是線段AB上方的拋物線上的一個動點.
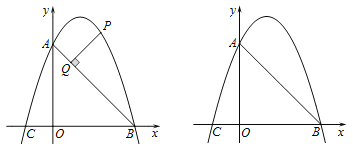
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 過點P作
過點P作![]() 于點Q,當線段PQ的長度最大時,求點P的坐標,和PQ最大值;
于點Q,當線段PQ的長度最大時,求點P的坐標,和PQ最大值;
![]() 過點P作x軸的垂線交線段AB于點M,再過點P作
過點P作x軸的垂線交線段AB于點M,再過點P作![]() 軸交拋物線于點N,請問是否存在點P使
軸交拋物線于點N,請問是否存在點P使![]() 為等腰直角三角形?若存在,求點P的坐標;若不存在說明理由.
為等腰直角三角形?若存在,求點P的坐標;若不存在說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個函數,如果它的自變量 x 與函數值 y 滿足:當1≤x≤1 時,1≤y≤1,則稱這個函數為“閉 函數”.例如:y=x,y=x 均是“閉函數”. 已知 y ax2 bx c(a0) 是“閉函數”,且拋物線經過點 A(1,1)和點 B(1,1),則 a 的取值范圍是______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com