
【題目】如圖1,P(2,2),點A在x軸正半軸上運動,點B在y軸上運動,且PA=PB.
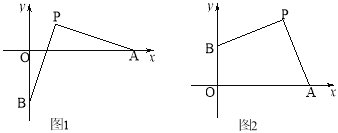
(1)求證:PA⊥PB;
(2)若點A(8,0),求點B的坐標;
(3)求OA – OB的值;
(4)如圖2,若點B在y軸正半軸上運動時,直接寫出OA+OB的值.
【答案】(1)詳見解析;(2)點B的坐標為(0,-4);(3)4;(4)4.
【解析】
試題分析:(1)過點P作PE⊥x軸于E,作PF⊥y軸于F,根據點P的坐標可得PE=PF=2,然后利用“HL”證明Rt△APE和Rt△BPF全等,根據全等三角形對應角相等可得∠APE=∠BPF,然后求出∠APB=∠EPF=90°,再根據垂直的定義證明;(2)求出AE的長度,再根據全等三角形對應邊相等可得AE=BF,然后求出OB,再寫出點B的坐標即可;(3)根據全等三角形對應邊相等可得PE=PF,再表示出PE、PF,然后列出方程整理即可得解;(4)同(3)的思路求解即可.
試題解析:(1)如圖1,過點P作PE⊥x軸于E,作PF⊥y軸于F
∵ P(2,2)
∴ PE=PF=2,∠EPF=90°
在Rt△APE和Rt△BPF中
![]()
∴ Rt△APE≌Rt△BPF(HL)
∴ ∠APE=∠BPF
∴ ∠APB=∠APE+∠BPE=∠BPF+∠BPE=90°
∴ PA⊥PB
(2)∵P(2,2)
∴ OE=OF=2
∵ A(8,0)
∴ OA=8
∴ AE=OA-OE=8-2=6
又由⑴得Rt△APE≌Rt△BPF
∴ BF=AE=6
∴ OB=BF-OF=6-2=4
∴ 點B的坐標為(0,-4)
(3)∵ Rt△APE≌Rt△BPF
∴ AE=BF
∵ AE=OA-OE=OA-2
BF=OF+OB= 2 +OB
∴ OA-2= 2 +OB
∴ OA -OB= 4
(4)OA +OB=4


科目:初中數學 來源: 題型:
【題目】《楊輝算法》中有這么一道題:“直田積八百六十四步,只云長闊共六十步,問長多幾何?”意思是:一塊矩形田地的面積為864平方步,只知道它的長與寬共60步,問它的長比寬多了多少步?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,點D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度數;(2)若∠ACB為α,則∠ECD的度數能否用含α的式子來表示.
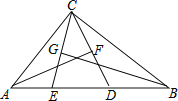
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,AD⊥BC于點D,點E為AC中點且BE平分∠ABD,連接BE交AD于點F,且BF=AC,過點D作DG∥AB,交AC于點G.
求證:
(1)∠BAD=2∠DAC
(2)EF=EG.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校學生會準備調查七年級敘述參加“繪畫類”、“書法類”、“樂器類”四類校本課程的人數,在全校進行隨機抽樣調查,并根據收集的數據繪制了如圖兩幅統計圖(信息尚不完整),請根據圖中提供的信息,解答下面的問題: 
(1)此次共調查了多少名同學?
(2)將條形圖補充完整,并計算扇形統計圖中樂器部分的圓心角的度數;
(3)如果該校共有1000名學生參加這4個課外興趣小組,而每個教師最多只能輔導本組的25名學生,估計書法興趣小組至少需要準備多少名教師?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com