Question

閱讀材料：

如圖1，AB、CD交于點O，我們把△AOD和△BOC叫做對頂三角形．
結論：若△AOD和△BOC是對頂三角形，則∠A+∠D=∠B+∠C．
結論應用舉例：
如圖2：求五角星的五個內角之和，即∠A+∠B+∠ACE+∠ADB+∠E的度數．
解：連接CD，由對頂三角形的性質得：∠B+∠E=∠1+∠2，
在△ACD中，∵∠A+∠ACD+∠ADC=180°，
即∠A+∠3+∠1+∠2+∠4=180°，
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五個內角之和為180°．
解決問題：
（1）如圖①，∠A+∠B+∠C+∠D+∠E+∠F=______；
（2）如圖②，∠A+∠B+∠C+∠D+∠E+∠F+∠G=______；
（3）如圖③，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=______；
（4）如圖④，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=______；
請你從圖③或圖④中任選一個，寫出你的計算過程．

Answer 1

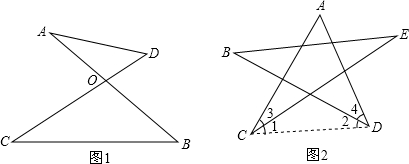
解：（1）連接CD，由對頂角三角形可得∠A+∠B=∠BDC+∠ACD，則∠A+∠B+∠C+∠D+∠E+∠F=360°；

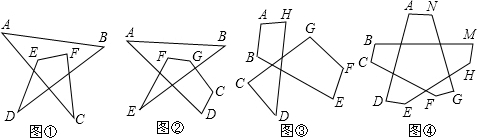
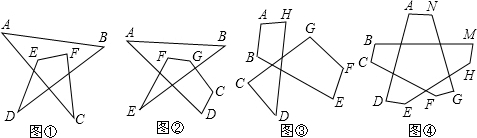
（2）連接ED，由對頂角三角形可得∠A+∠B=∠BED+∠ADE，則∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°；

（3）連接BH、DE，
∵由對頂角三角形可知∠EBH+∠BHD=∠HDE+∠BED，
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=五邊形CDEFG的內角和+△ABH的內角和=540°+180°=720°；

（4）連接ND、NE，
∵由對頂角三角形可知∠1+∠2=∠NGH+∠EHG，
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=六邊形BCFGHM的內角和+△AND的內角和+△NDE的內角和=（6-2）×180°+360°=1080°．

故答案為：360°；540°；780°；1080°．
分析：（1）連接CD，由對頂角三角形可得∠A+∠B=∠BDC+∠ACD，再由四邊形的內角和定理得出結論；
（2）連接ED，由對頂角三角形可得∠A+∠B=∠BED+∠ADE，再由五邊形的內角和定理得出結論；
（3）連接BH、DE，由對頂角三角形可知∠EBH+∠BHD=∠HDE+∠BED，再根據五邊形的內角和定理得出結論；
（4）連接ND、NE，由對頂角三角形可知∠1+∠2=∠NGH+∠EHG，再由六邊形的內角和定理得出結論．
點評：本題考查的是三角形內角和定理，根據題意作出輔助線，利用△AOD和△BOC叫做對頂三角形的性質及多邊形的內角和定理解答是解答此題的關鍵．