Question

如圖所示，已知等腰△ABC中AB=AC，AD是△ABC的角平分線，E是AC延長線上一點，且CE=CD，AD=DE．
（1）求證：△ABC是等邊三角形；
（2）如果把AD改為△ABC的中線或高，（其它條件不變）請判斷（1）中結論是否依然成立？（不要求證明）

Answer 1

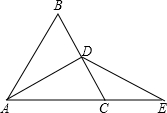
（1）證明：∵CD=CE，∴∠E=∠CDE，
∴∠ACB=2∠E．
又∵AD=DE，∴∠E=∠DAC，
∵AD是△ABC的角平分線，
∴∠BAC=2∠DAC=2∠E，
∴∠ACB=∠BAC，∴BA=BC．
又∵AB=AC，∴AB=BC=AC．
∴△ABC是等邊三角形．

（2）解：當AD為△ABC的中線或高時，結論依然成立．
分析：（1）根據等腰三角形的性質可得，角平分線AD同時也是三角形ABC底邊BC的高，即∠ADC=90°． 再加上已知條件可推出∠DAC=30°，即可知三角形ABC是等邊三角形．（2）在等腰三角形ABC中，如果其他條件不變，則AD同時是角平分線、中線及高，所以（1）中結論仍然成立．
點評：此題主要考查了等邊三角形的判定，綜合利用了等腰三角形和直角三角形的性質． 同時要掌握等腰三角形中底邊的高、中線和角平分線重合的性質．